MathMaster Blog

Multiplying radicals implies the use of the Product and Quotient rules.

According to the Product Rule, the product of two or more numbers raised to a power equals the product of each number raised to the same power.

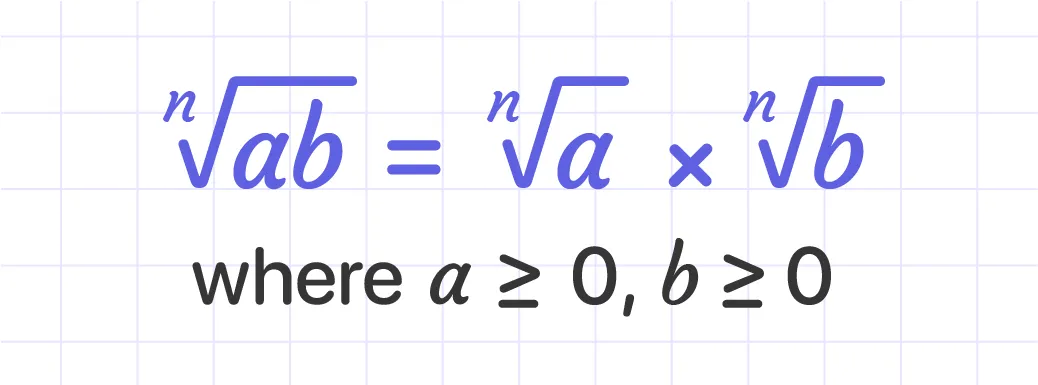
The Quotient Rule states that the radical of a quotient is equal to the quotient of the radicals of the numerator and denominator.

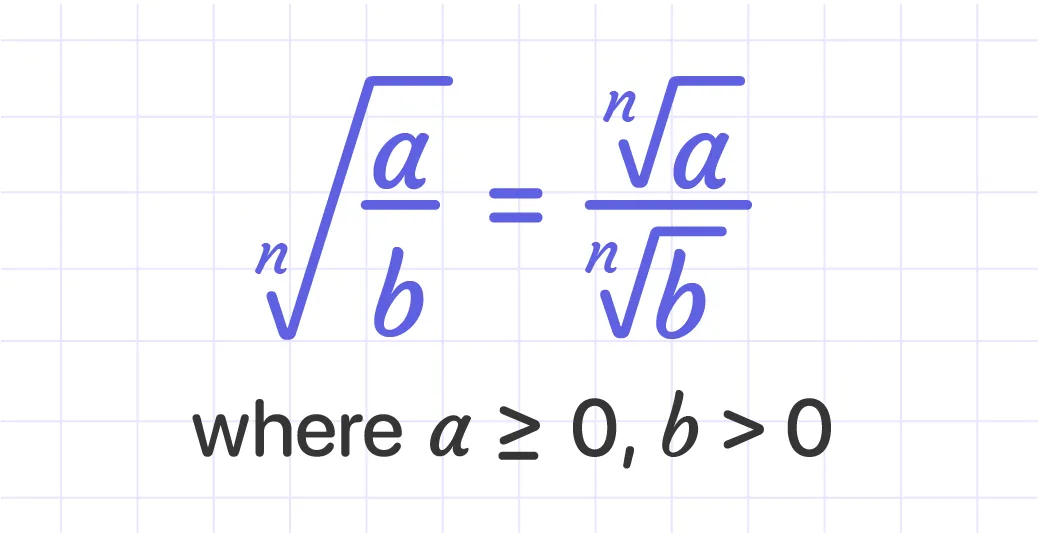
When multiplying radicals (with the same index), multiply under the radical first, then in front of it.

Example 1:

Multiply:$5\sqrt{5} \times 3\sqrt{10}$

Solution:

Multiply out front and multiply under the radicals:

$5\sqrt{5} \times 3\sqrt{10} = 15\sqrt{50}$

Then, simplify the result:

$15\sqrt{50} = 15\sqrt{2 \times 25} = 15\sqrt{2} \times 5\sqrt{2} = 75\sqrt{2}$

Answer: $75\sqrt{2}$