MathMaster Blog

In mathematics, exploring what is a prime number is a fundamental pursuit that engages students, professionals, and mathematicians' intellects. Defined as natural numbers exceeding 1 and possessing solely two distinct divisors—1 and themselves—prime numbers are pivotal in number theory. This exclusive characteristic makes prime numbers intriguing study subjects for students, professionals, and mathematicians alike. This article embarks on a rigorous journey to elucidate the essence of prime numbers, providing insights into their significance and the methods employed to identify them.
What Is a Prime Number: Examples
Prime numbers exhibit an unmistakable pattern of divisibility. Some classic examples of prime numbers include:
- 2 — two
- 3 — three
- 5 — five
- 7 — seven
Prime Numbers 1 to 10
Exploring the prime numbers 1 to 10, prime number examples unveil a handful of foundational primes. Notably, the list comprises the numbers 2, 3, 5, and 7. These prime entities form the building blocks for deeper insights into number theory.
Prime Numbers 1 to 100
Prime numbers 1 to 100 broaden the scope of our understanding. This range includes an array of prime number examples, such as 11, 13, 17, 19, and so forth. The diverse distribution of prime numbers within this range highlights their essential role in number theory and their implications across various mathematical disciplines.
In Prime Numbers 1 to 100:
- 2 — two
- 3 — three
- 5 — five
- 7 — seven
- 11 — eleven
- 13 — thirteen
- 17 — seventeen
- 19 — nineteen
- 23 — twenty-three
- 29 — twenty-nine
- 31 — thirty-one
- 37 — thirty-seven
- 41 — forty-one
- 43 — forty-three
- 47 — forty-seven
- 53 — fifty-three
- 59 — fifty-nine
- 61 — sixty-one
- 67 — sixty-seven
- 71 — seventy-one
- 73 — seventy-three
- 79 — seventy-nine
- 83 — eighty-three
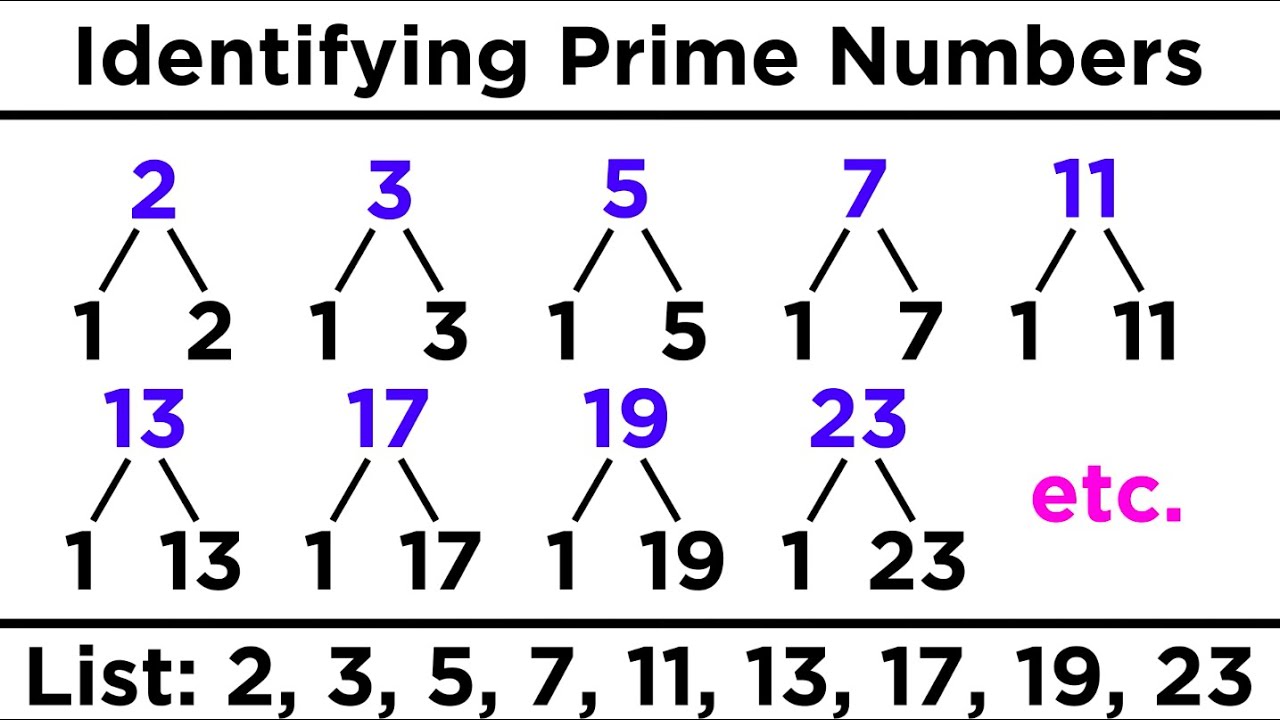
How to Find Prime Numbers
The process of discovering prime numbers is a complex and intricate one that requires a deep understanding of mathematical algorithms and techniques. One must thoroughly comprehend prime factorization, sieving methods, and the Sieve of Eratosthenes to identify prime numbers successfully. These tools are crucial for individuals searching for these numbers, whether students or professionals. Mastering these techniques can significantly enhance their ability to identify and work with prime numbers.
The History of Prime Numbers
Delving into the historical context of prime numbers uncovers a narrative intertwined with the evolution of mathematical thought. From the ancient Greeks to modern scholars, the exploration of prime numbers has left an indelible mark on mathematical discourse.
The Distribution of Prime Numbers
Analyzing the distribution of prime numbers reveals intriguing patterns and irregularities. The prime number theorem, formulated by mathematicians like Gauss and Riemann, sheds light on the density of primes as numbers grow larger, offering insights into their fundamental nature.The Uses of Prime Numbers in Cryptography
Beyond theoretical mathematics, prime numbers find practical applications in cryptography. Their role in encryption algorithms, such as RSA, underscores their significance in securing digital communication and safeguarding sensitive information.
The Applications of Prime Numbers in Computer Science
In computer science, prime numbers play a crucial role in a wide range of algorithms and computations. These unique mathematical entities are used in many different applications, including hashing functions and randomized algorithms. By leveraging the properties of prime numbers, computer systems are able to operate with greater efficiency and reliability, delivering optimal results and helping to ensure the security of digital communication and sensitive data.
The Challenges of Finding Prime Numbers
Unraveling the complexities inherent in prime numbers presents mathematicians with substantial challenges. The endeavor to identify these distinct numerical entities, mainly when dealing with larger values, introduces intricate computational obstacles. As numerical magnitudes increase, the task of determining their primality becomes progressively demanding, requiring the application of advanced algorithms and computational resources.
Distinguishing prime numbers, especially those of significant size, involves intricate mathematical and computational considerations. The sheer volume of potential divisors to be examined for larger numbers contributes to the complex nature of the task. This complexity grows exponentially as numbers ascend, adding to the computational load. Consequently, researchers and mathematicians must consistently develop innovative methodologies, utilizing technology and mathematical expertise to navigate this intricate landscape and accurately and efficiently identify prime numbers.
The Open Problems in Prime Number Theory
Despite centuries of exploration, prime numbers continue to pose intriguing unsolved problems. Questions surrounding the distribution of prime pairs, the twin prime conjecture, and the Goldbach conjecture inspire mathematicians to push the boundaries of mathematical understanding.
MathMaster: An App that makes solving and Finding Prime Numbers Easy
MathMaster is an exceptional app that can assist with solving a wide range of mathematical problems, including statistical calculations and prime numbers. With its fast and user-friendly interface, Math Master is an excellent resource for simplifying complex numerical computations. Whether you're a student needing assistance or an avid learner looking to conquer mathematical challenges, Math Master offers comprehensive guidance and support to help you achieve your goals. So why struggle with complex arithmetic problems when Math Master can make the process significantly more accessible? Give it a try today and experience the benefits for yourself! What is a prime number? That's no longer a problem with MathMaster!
Conclusion
In conclusion, prime numbers, and what is a prime number, are captivating entities that engage the minds of students, professionals, and mathematicians alike. Their unique properties, historical significance, and practical applications underscore their enduring importance in mathematics and beyond. As we persist in delving into the depths of number theory, the enigma of prime numbers will undoubtedly remain a cornerstone of mathematical inquiry.