MathMaster Blog

For those preparing for the ACT, the math section is often the most troubling. Without the right preparation, it can be easy to get lost in the complex equations and story problems that are presented on the test.

The good news is that the hardest ACT math questions can be practiced and perfected. To provide aid to those preparing for ACT math, we have pulled together the top five hardest ACT math problems.

ACT Math Question #1 – Number and Quantity

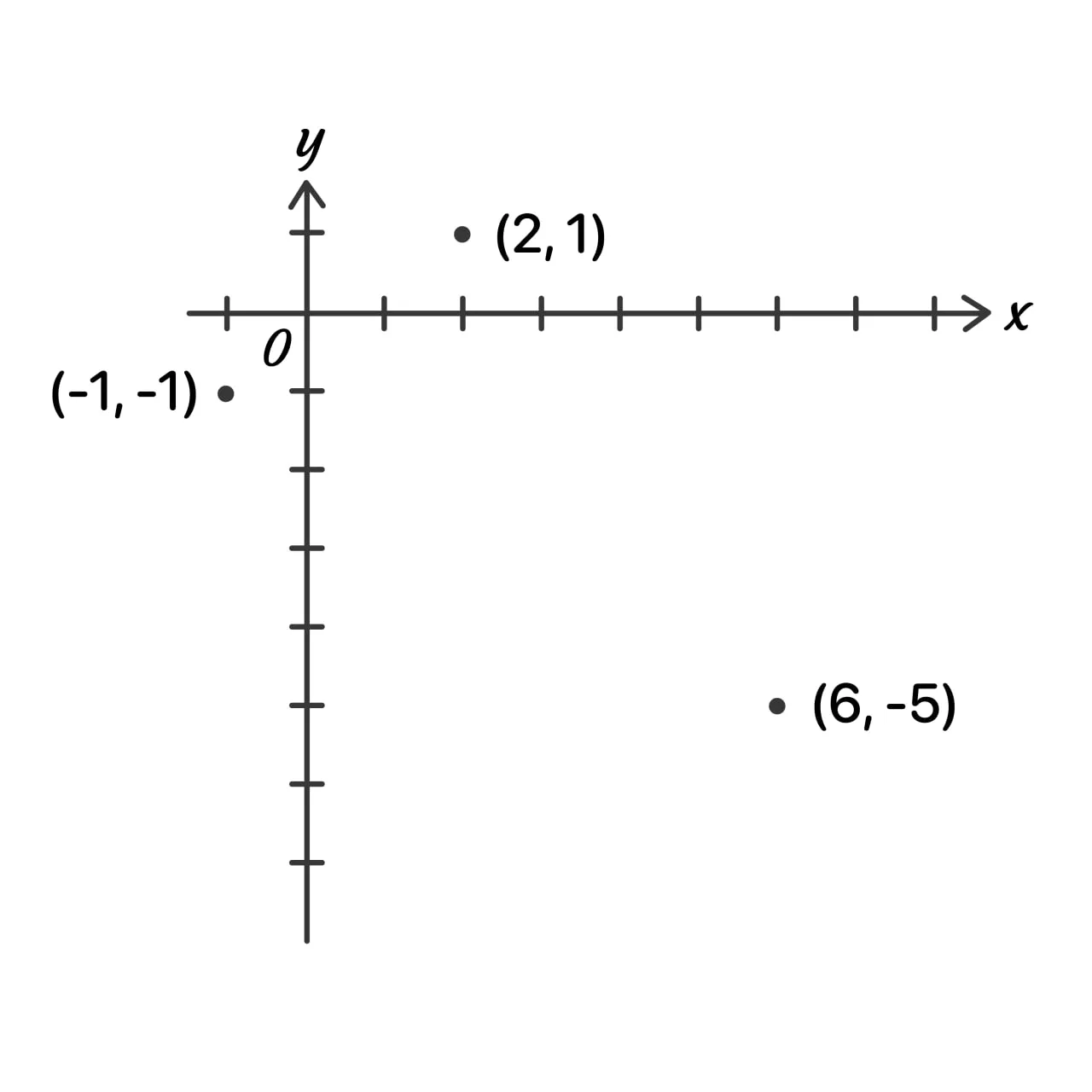
In the standard (x,y) coordinate plane below, 3 of the vertices of a rectangle are shown. Which of the following answers displays the 4th vertex of the rectangle?

a. (3,-7)

b. (4,-8)

c. (5,-1)

d. (8,-3)

e. (9,-3)

Correct Answer: a.

How to Solve it:

1. This question can be solved by calculating the slope.

2. As shown in the graph, one must move up 2 units and right 3 units to travel from point (-1,-1) to (2,1).

3. This would give us a slope for the shorter side of the rectangle to be 3/2.

4. By using the slop as a formula, we can realize the equations of both the x and y values:

• X value: 6 – 3 = 3
• Y value: -5 – 2 = -7

5. The fourth vertex is located at (3,-7).

ACT Math Question #2 – Algebra

If h(x) = x³ + x and g(x) = 2x + 3, then g(h(2)) = ?

a. 7

b. 10

c. 17

d. 19

e. 23

Correct Answer: e.

How to Solve it:

1. This equation is essentially asking for the value of g(x) when x is equal to h(2). To solve, simply plug 2 in for x in h(x) and then plug that value in for x in g(x).

2. Plugging 2 in for x in h(x): h(2) = 2³ + 2 finds the answer 10.

3. Plugging 10 in for x in g(x: (g(10) = 2(10) + 3 finds the answer 23.

ACT Math Question #3 – Statistics and Probability

What is the probability that a number selected at random from the set {2, 3, 7, 12, 15, 22, 72, 108} will be divisible by both 2 and 3?

a. 1/4

b. 3/8

c. 3/5

d. 5/8

e. 7/8

Correct Answer: b.

How to Solve it:

1. The solution to this problem is straightforward: simply go through the set of numbers and count how many are divisible by both 2 and 3.

• Divisible by both 2 and 3: 12, 72, 108.
• Not divisible by both 2 and 3: 2, 3, 7, 15, 22.

2. Out of the 8 numbers presented, 3 are divisible by both 2 and 3, leaving us with an answer of 3/8.

ACT Math Question #4 – Statistics and Probability

The 35-member Math Club is meeting to choose a student government representative. The members decide that the representative, who will be chosen at random, cannot be any of the 3 officers of the club. What is the probability that David, a member but not an officer, will be chosen?

a. 0

b. 4/35

c. 1/35

d. 1/3

e. 1/32

Correct Answer: e.

How to Solve it:

1. The solution to this ACT math problem is fairly straightforward. The solution can be found in the list of possible answers and requires little math to be performed.

2. All we need to do is choose the correct numerator and denominator. Since we only determine the probability for one officer, we know the numerator must be 1. The denominator represents the possible choices as a whole. Since we know that the possible choices exclude only the 3 officers, and the total club member number is 35, we know the denominator is 32. This gives us an answer of 1/32 for the probability of David becoming the representative.

ACT Math Question #5 – Modeling

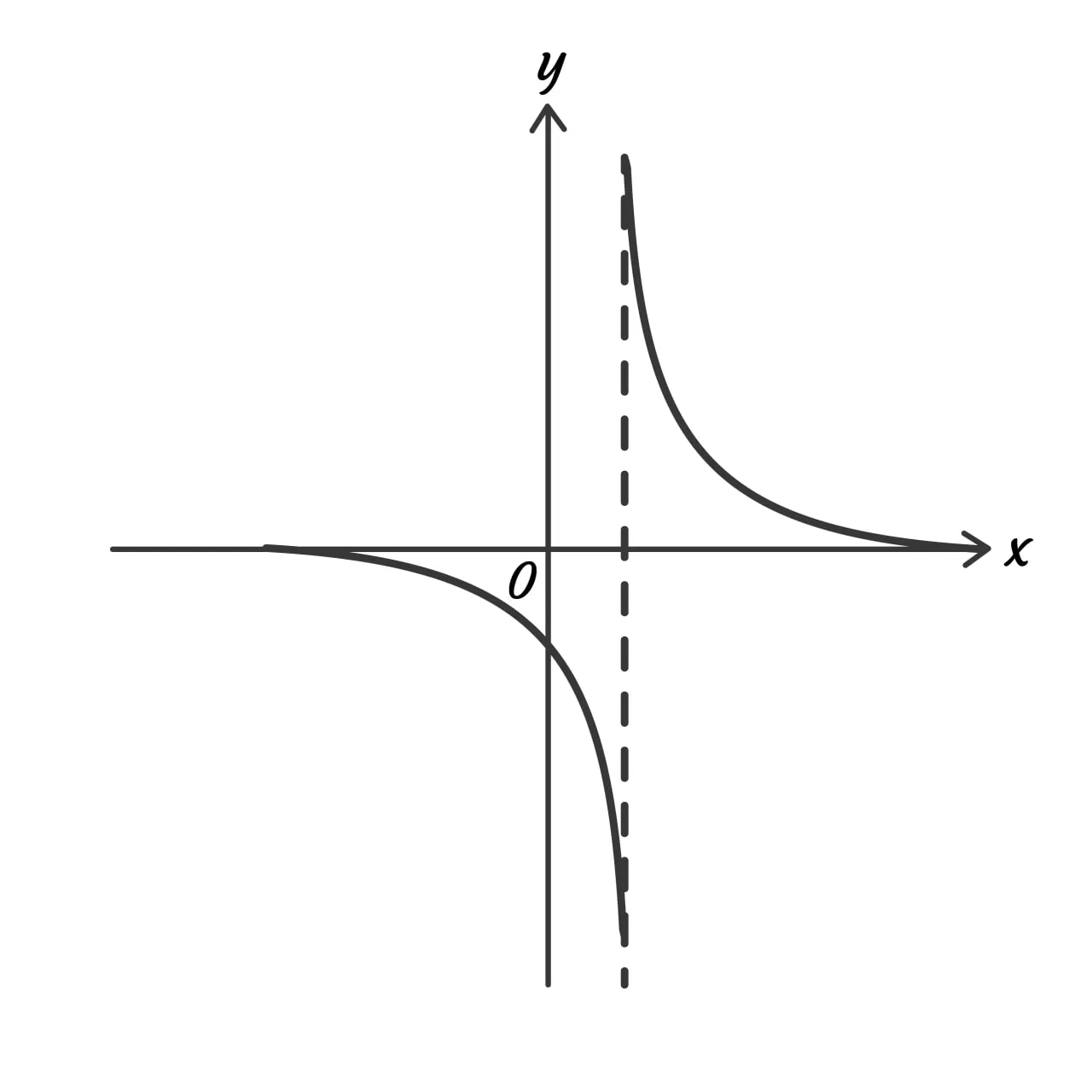
The graph of a given hyperbola, y = h(x), is shown in the standard (x,y) coordinate plane below.

Among the following graphs, which best represents y = -h(x)?

Correct Answer: F

How to Solve it:

1. In this ACT math problem, we are looking for the inverted or negative version of the first graph. Since we are given no specific equations, we must solve the problem visually.

2. We can immediately dismiss the answers H, I, and J as their slopes do not match the original graph.

3. Choosing between graphs F and G requires a closer look. However, after realizing the limits of graph G were shifted on the X axis, it becomes obvious that cannot be the answer By process of elimination, we are left with F as our answer.

The Best ACT Math Questions Help – MathMaster

If you are looking for some additional help with your ACT math preparation, you’ll love the free tools MathMaster has to offer. With MathMaster’s advanced problem solver and test prep, you’ll be able to get unstuck from even the hardest ACT math questions. Be sure to check out our innovative app, MathMaster, in the Appstore today!