What Are Cube Numbers?

In the realm of mathematics, numbers are more than mere symbols. They possess unique characteristics and properties that have intrigued mathematicians for centuries. Cube numbers are one such fascinating concept that has left many curious minds pondering.
This article will delve deep into the world of cube numbers, exploring their definition, properties, and practical applications. So, what are these numbers, and why are they so intriguing? Let's find out.
Understanding Cube Numbers
What Are Cube Numbers?
Cube numbers, also known as perfect cubes, are a special class of numbers that result from multiplying an integer by itself twice. In mathematical terms, the cube number is the cube of an integer, which can be represented as n3, where "n" is the integer. To put it simply, the cube of a number is the product of multiplying a number by itself three times. For instance, if you take the integer 2 and multiply it by itself twice (2 × 2 × 2), you get the cube number 8.
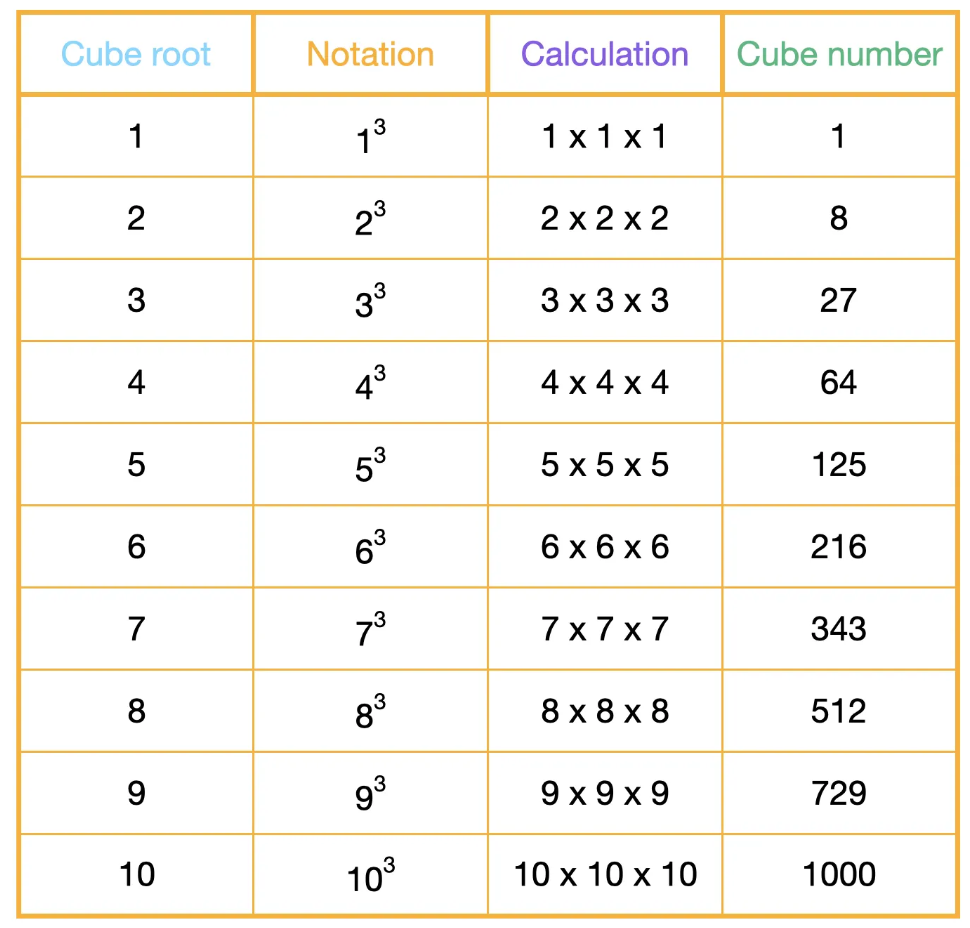
How to Calculate the Cube of a Number
Cubing a number is a mathematical operation that involves raising a number to the power of 3, or in simpler terms, multiplying it by itself twice. Here's a step-by-step guide on how to cube a number:
- Select a Number: Begin by choosing the number you want to cube. Let's say you want to cube the number 4.
- Write the Expression: Express the cubing operation as an exponentiation. In this case, it would be 43.
- Calculate: Calculate the result by performing the multiplication. In our example, 43 equals 4 x 4 x 4, which equals 64.
So, cubing the number 4 gives us the result of 64. You can use this method to cube any integer. Cubing is commonly encountered in various mathematical and scientific calculations, particularly in geometry for volume calculations and in physics for equations involving the cube of physical quantities. It's a fundamental operation that helps us effectively understand and work with cube numbers.
Properties of Cube Numbers
- Distinctive Shape: Cube numbers derive their name from their geometric shape. When objects are arranged in the shape of a cube, each side contains the same number of objects as the cube number itself. For example, if you have a cube with 8 objects on each side, it represents the cube number 8. This unique correspondence between the number and the geometric shape is a defining characteristic of cube numbers.
- Odd and Even: Cube numbers exhibit diversity in their parity, meaning they can be both odd and even. For instance, 8 and 64 are cube numbers, and they are all even. Conversely, numbers that are cubed, like 1 and 27, are odd. This versatility adds to the richness of cube numbers in mathematical analysis.
- Ascending Sequence: Numbers that are cubed follow a straightforward and continuous ascending sequence. They commence with the smallest possible cube number, which is 1 (13), and extend infinitely as you increase the value of "n." This sequential nature provides a clear understanding of what are cube numbers and, how they are generated, and their progression in numerical order.
- Cubed Meaning in Math: In mathematics, the term "cubed" is used to indicate raising a number to the power of 3. When you cube a number, you are essentially multiplying it by itself three times. For instance, "2 cubed" (23) equals 8. This fundamental operation is at the heart of cube numbers and plays a crucial role in cubed meaning in math and computation.
Practical Applications of Cube Numbers
These numbers find applications in various fields, including mathematics, science, and engineering:
- Volume Calculations: In geometry, cube numbers are used to calculate the volume of cubes and rectangular prisms. By knowing the side length of a cube (which is usually a cube number), you can easily find its volume.
- Engineering: The cube of numbers is essential in engineering when dealing with three-dimensional structures, such as designing buildings or calculating the capacity of containers.
- Physics: In physics, cube numbers are involved in equations related to the cube of a physical quantity, like displacement or velocity. Number Patterns: The cube of numbers is a part of various number patterns and sequences, which are studied extensively in mathematics.
If you find yourself in need of assistance with various math problems, including what are cube numbers or any other mathematical challenges, consider utilizing the innovative math-solving tool MathMaster. Whether you're dealing with cube numbers, square numbers, or complex equations, MathMaster can be your go-to app for efficient and accurate mathematical solutions. Say goodbye to math-related struggles and let MathMaster simplify your mathematical journey, making it more enjoyable and efficient.
Final Thoughts
Cube numbers are a captivating aspect of mathematics that serve a variety of purposes in the real world. They are not just theoretical entities but find practical applications in various fields. Understanding cube numbers and their properties can lead to a deeper appreciation of the mathematical world around us.
So, the next time you encounter the question of what are cube numbers, remember that it's more than just a number—it's a glimpse into the intriguing world of mathematical patterns and relationships.