What Are Composite Numbers?

Numbers in mathematics are categorized into several classes. They can be whole numbers, prime numbers, rational numbers, complex numbers, composite numbers, and other categories. However, numbers 0, 1, 2, 3, 4, 5, 6, 7,8, and 9 are classified based on the number of factors they have. For instance, a number that contains only two factors -1 and the number itself is considered a prime number. A number with more than two factors is composite. This article will explain what is a composite number, including its properties, factors, significance, and how to identify one.
What is a Composite Number?
A composite number is a number with 3 or more factors. It can also be defined as a number that is divisible by more than two numbers or at least one number other than 1 and the number itself. A composite number is simply the opposite of a prime number.
Composite Numbers Definition: A positive integer or a natural number that has more than two factors
Examples of Composite Numbers
The smallest composite numbers that you will encounter are 4, 6, 8, 9, and 10. Each has at least three factors. Here are some specific composite number examples:
- 4 is divisible by 1,2, and 4.
- 8 is divisible by 1,2,4, and 8.
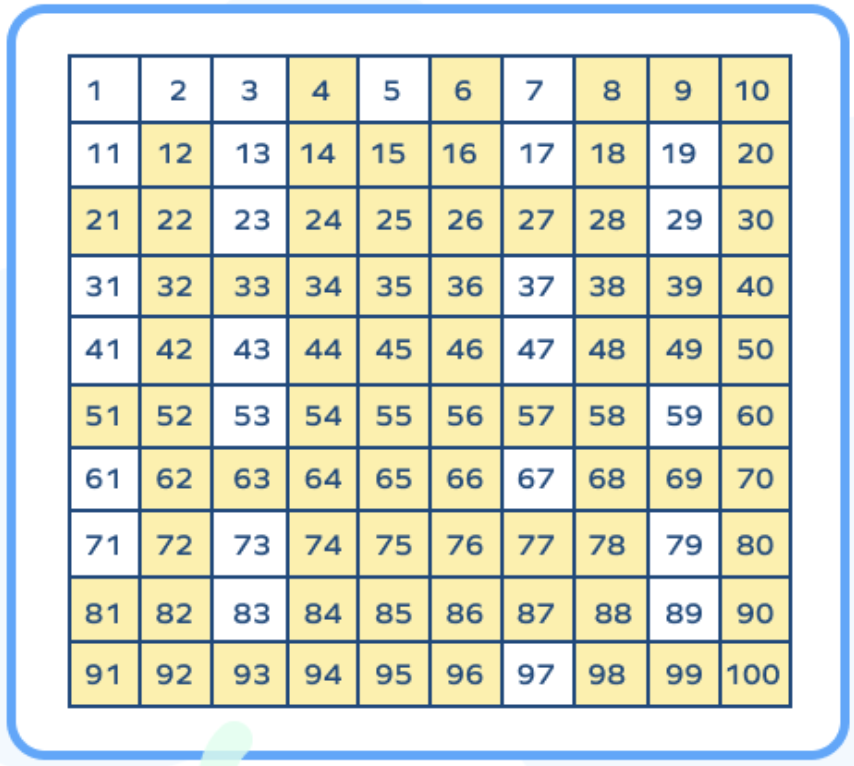
The following table summarizes the composite numbers from 1 to 100 comprehensively. While there are only five composite numbers between 1-10, they are 74 composite 1 to 100:
| Composite Numbers 1 to 10 | Composite Numbers 1 to 100 |
|---|---|
| There are Five composite numbers between 1 and 10 | There are 74 composite numbers between 1 to 100 |
| 4, 6, 8, 9, 10 | 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100 |
How to Find Composite Numbers
To find a composite number:
- Find the factors of the given number.
- If the number has only two factors, 1 and the number itself, then it is a prime number.
- If the number has more than two factors, it is a composite number.
The best way to identify a composite number is to do a divisibility test. The test helps to determine if the given number is a prime number or a composite number. The divisibility test shows that a number can be divided by another number (other than 1 and itself) completely with no remainder.
Properties of Composite Numbers
For a number to be called a composite number, it should have the following properties:
- A composite number has 3 or more factors.
- Composite numbers are positive integers.
- Each composite number is made up of two or more prime numbers.
- Composite numbers must be divisible by other composite numbers.
- Composite numbers should be completely divisible by smaller numbers whether composite or prime.
To understand the properties of composite numbers, take 36 as an example.
How 36 is an example of a composite number
| The factors of 36 | 1, 2, 3, 4, 6, 9, 12, 18, and 36 |
|---|---|
| The prime factorization of 36 | 2 × 2 × 3 × 3 |
| The prime factors of | 36 = 2² × 3² |
When you multiply the positive integers above, you get a composite number. Simply stated, 36 is a composite number that has two prime numbers as a factor and is evenly divisible by nine numbers.
Types of Composite Numbers
For you to understand the types of composite numbers, you must first understand the concept of even and odd numbers. An even number is defined as a number that is evenly divisible by two without leaving a remainder. On the other hand, a number that is not completely divided by two is known as an odd number. Consequently, composite numbers are classified into two:
- Even composite numbers
- Odd composite numbers
Let’s have a look at how the two types differ in relation to the concept of composite numbers:
Even Composite Numbers
A composite number that is also an even number is also called an even composite number. Therefore, all the even numbers that are not prime are even composite. Examples of composite even numbers include 4, 6, 8, 10, 12, 14, 16, 18, 20. These numbers are completely divisible by two and have more than 2 factors. Hence, they are even composite numbers.
Odd Composite Numbers
Odd composite numbers include all the odd numbers that are not prime numbers. The smallest odd composite number is 9. Considering the composite number examples between 1 and 30, the odd composite numbers include 9, 15, 21, 25, and 27 since they are not divisible by two.
Even Composite Numbers vs. Odd Composite Numbers
| A composite number that is also an even number | A composite number that is also an odd number |
|---|---|
| All the even numbers that are not prime | Odd numbers that are not prime |
| Examples include 4, 6, 8, 10, 12, 14, 16, 18, 20 | Examples include 9, 15, 21, 25, and 27 |
Smallest Composite Number
The smallest composite number is 4. This is because number 1 is neither a prime number nor a composite number since the sole divisor of 1 is 1. Numbers 2 and 3 are prime numbers because they can only be divided by 2 factors, 1 and the number itself. As such, 2 and 3 are not composite numbers. However, 4 has more than 2 factors 1,2, and 4. Therefore, 4 is the smallest composite number since it meets the criteria of composite numbers
Difference Between Prime and Composite Numbers
Composite numbers have more than two factors (1 and itself) while prime numbers have only two factors and can only be divisible by 1 and itself. Composite numbers can be written as the product of 2 or more numbers. On the contrary, prime numbers can only be written as a product of 2 numbers.
Applications of Composite Numbers in Mathematics
Other than identifying composite or prime numbers, primary students are not likely required to know that numbers are composite. Nevertheless, composite numbers are used in the field of mathematics for performing arithmetic, describing shapes objects quantifying, and even measuring.
Applications of Composite Numbers in Real-Life
Composite numbers are not useful in real life unless working in fields where prime numbers skills are essential like a primary school teacher or in cyber security or telecommunication.
MathMaster: A Math-Solving Platform That Makes Learning Composite Numbers Easy
MathMaster is a platform that makes solving math problems easy. If you find it difficult to understand composite numbers, prime numbers, and other math challenges, MathMaster is an innovative app that provides a solution to all your math questions. With MathMaster expert help in real time, all your mathematics questions are answered instantly.
Final thoughts
Understanding the concept of composite numbers and prime numbers is crucial. Composite numbers are useful in elementary functions such as subtraction, divisibility, and addition in school. However, breaking up composite numbers into their prime number factors can help solve a lot of puzzles in mathematics. One of the areas this is most applicable is cybersecurity where prime numbers are used in cryptography.