Integrals

Integrals are the values of the function obtained through the integration process. Integration is mostly used to compute the volumes of three-dimensional objects and to calculate the areas of two-dimensional regions.

There are two types of integrals:

Definite Integrals

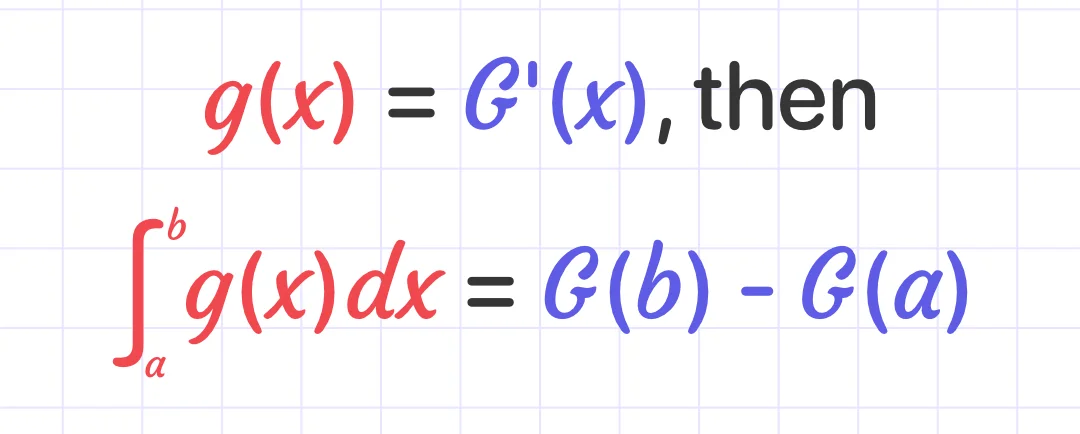
The definite integrals are used to calculate the area under a curve with respect to one of the coordinate axes and within the specified limits.

The definite integral formula is as follows:

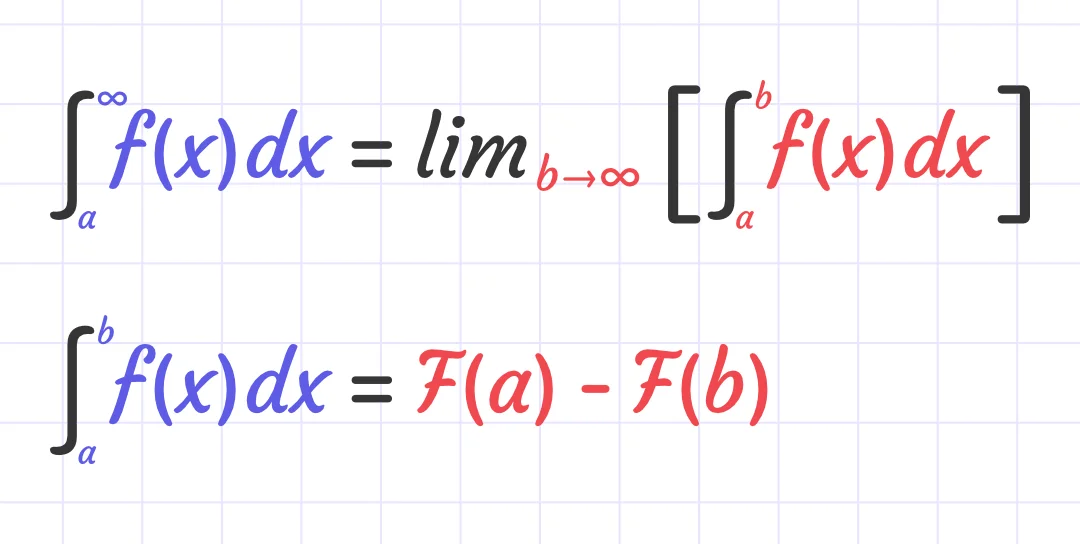
Indefinite Integrals

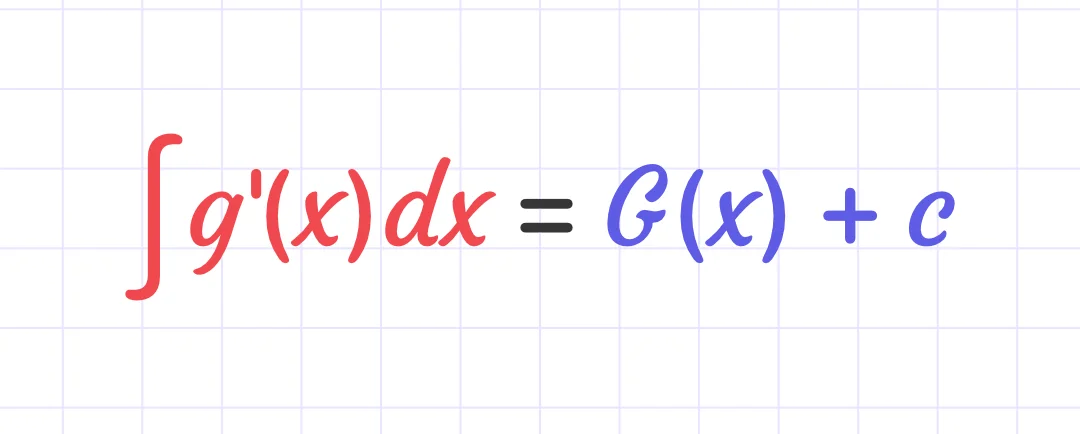
These integrals lack a pre-existing value of limits, making the final value of the integral indefinite.

There are various methods for calculating indefinite integrals:

Integration by substitution

If u is a function of x, then u' = du/dx.

Integration by parts

If two functions are of the product form,

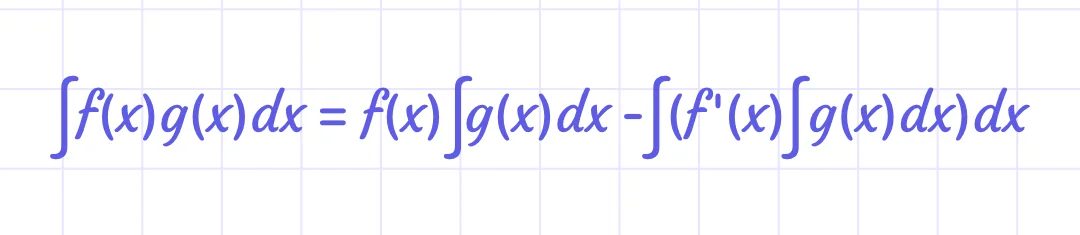
Integration by partial fractions

To find ∫ f(x)/g(x) dx, decompose this improper rational function to a proper rational function and then integrate.

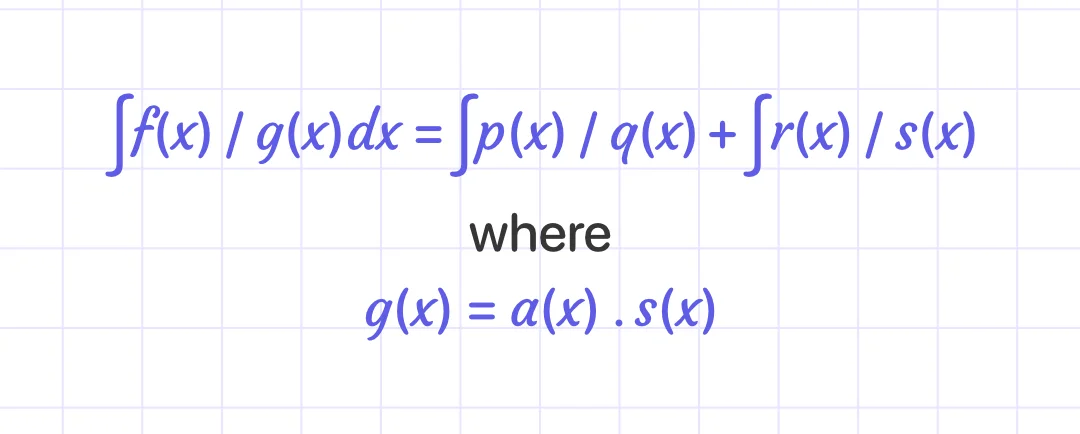
First Fundamental Theorem of Integrals

The integral of the derivative is the function; or, more precisely, it’s the difference between two outputs of that function.

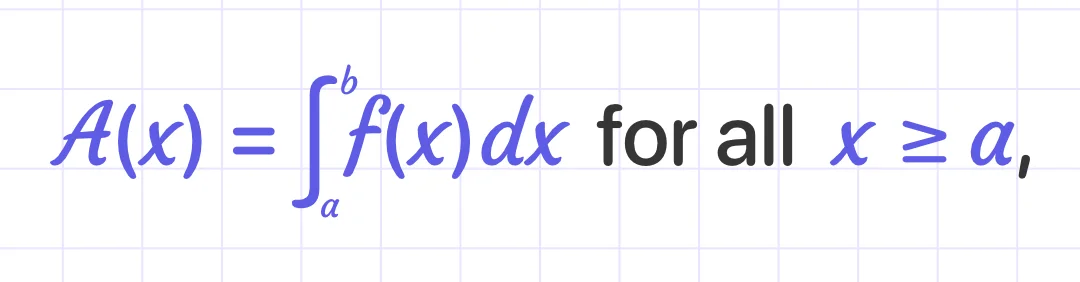
where the function is continuous on [a,b].

Then A'(x) = f(x) for all x ϵ [a,b].

Second Fundamental Theorem of Integrals

If f is a continuous function and c is any constant, then f has a unique antiderivative A that satisfies A ( c ) = 0, and that antiderivative is given by the rule

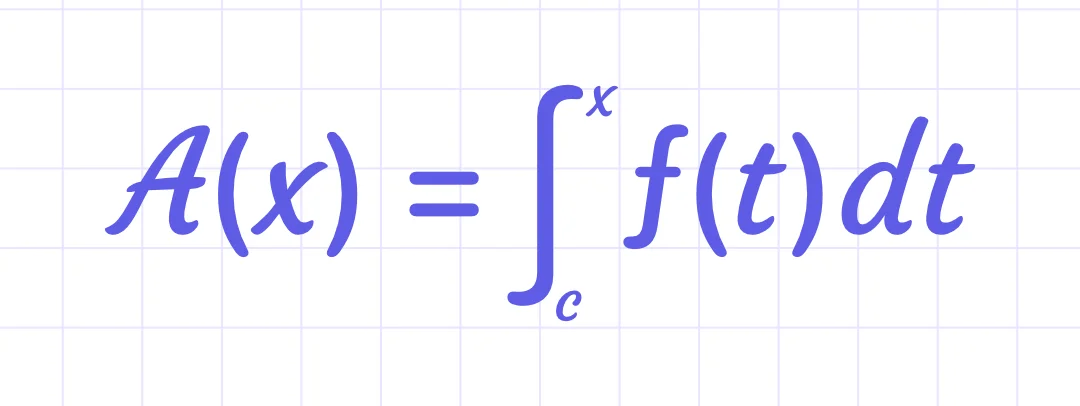
Example 1:

Calculate the definite integral:

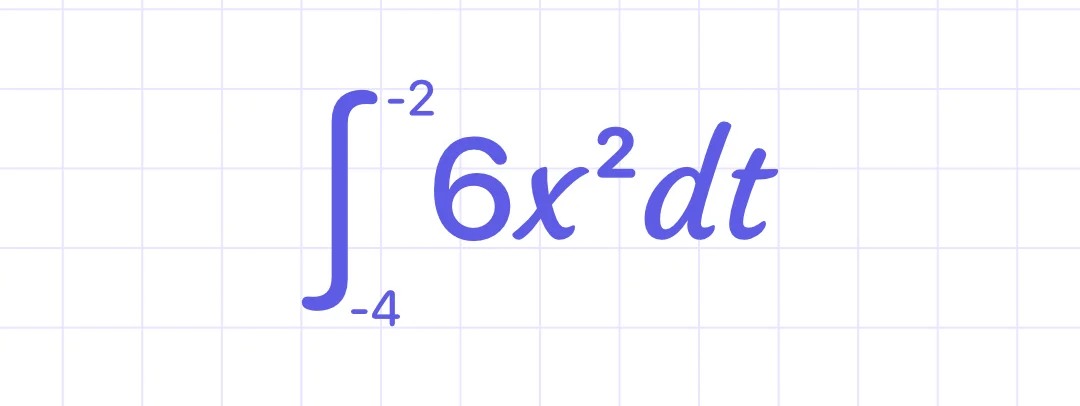
Solution:

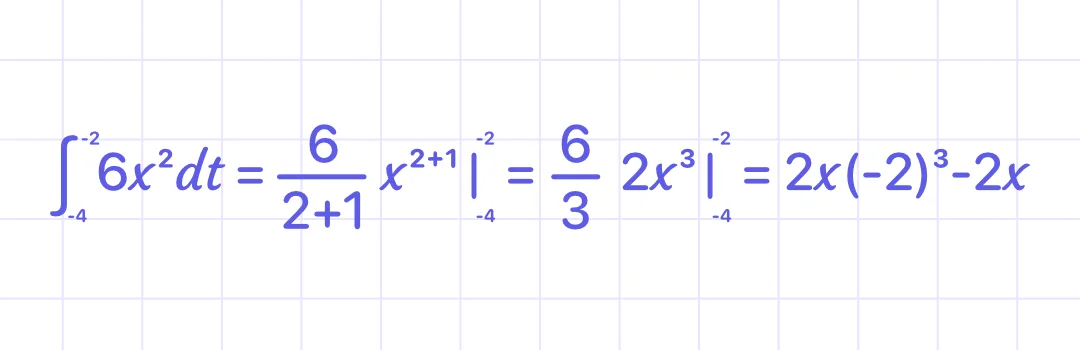
Answer: 112

Example 2:

Find the exact answer to $\int_1^2 \frac{xe^x - x^3 + 1}{x} dx$.

Show all work with an organized solution.

Solution:

Divide the fraction into single polynomial terms and finish integration following next rules:

1. ∫(f+-g)dx = ∫fdx +- ∫gdx+-...∫hdx
2. ∫xndx = (xn+1/(n+1) + c
3. ∫dx/x = ln(abs(x)) + c
4. ∫nxdxxdx = e x x+c

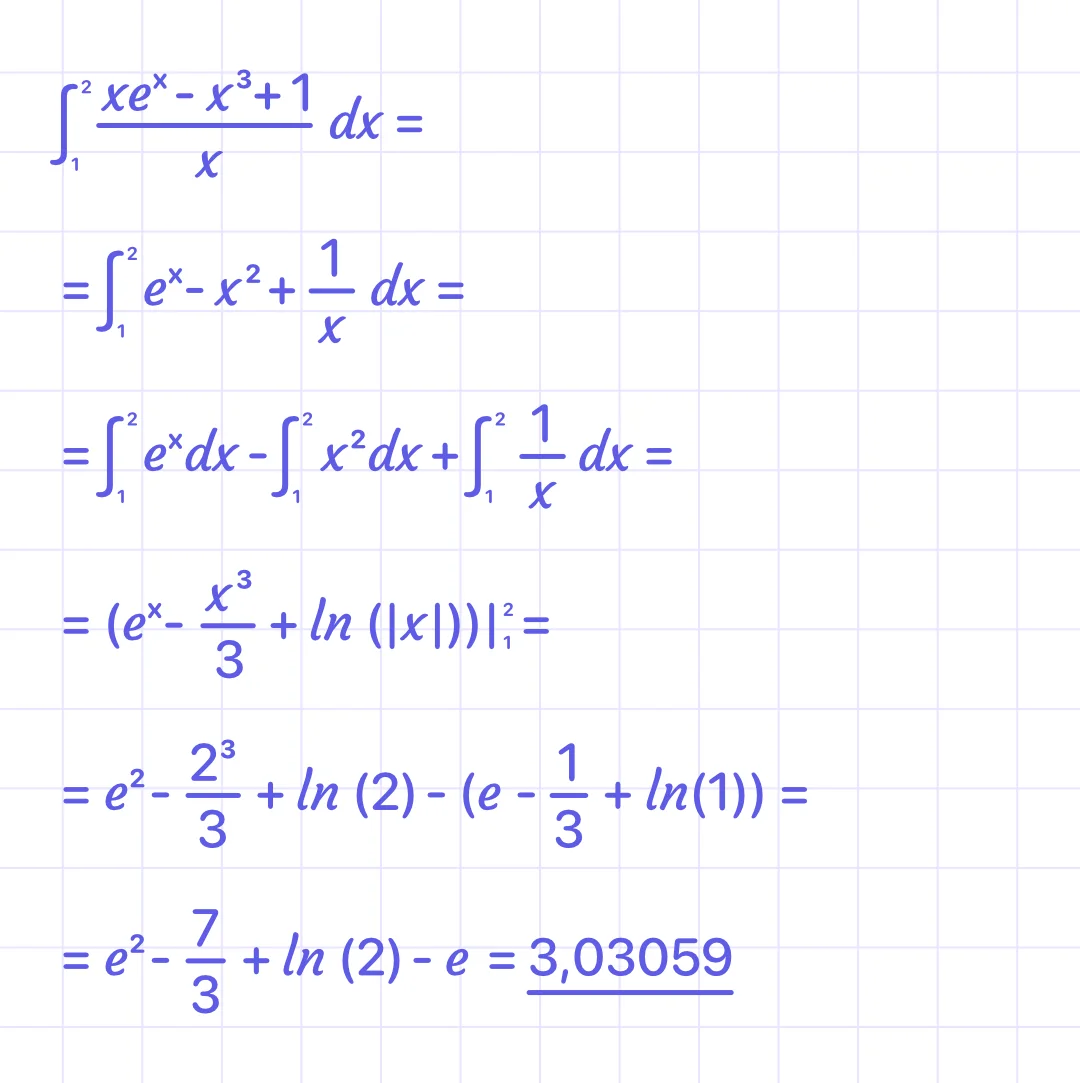
Answer: 3.03059