What Are Vertices, Faces, and Edges? A Profound Exploration of Geometric Fundamentals

In geometry, a deep understanding of vertices, faces, and edges is essential. These foundational elements resonate not only with mathematicians but also with educators and professionals navigating the intricate landscape of geometry. In this article we’ll find out:
- what the basics of vertices, faces, and edges are;
- why knowing these geometrical concepts is essential for primary school learners;
- how these concepts can be applied in computer science;
- how we can use this knowledge in our everyday lives.
Let’s start!
Understanding the Basics of Vertices, Faces, and Edges individually
Vertices
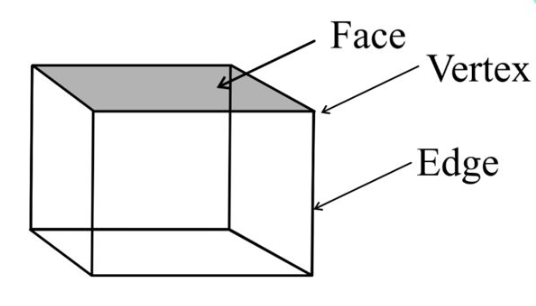
At the heart of geometric shapes are vertices. A vertex is a point where two or more edges meet, essentially serving as a corner or junction. In a two-dimensional (2D) shape like a triangle, vertices mark the endpoints of its sides. When it comes to three-dimensional (3D) shapes such as cubes or pyramids, vertices form the critical intersections of edges.
Vertex of cube
The cube is one type of polyhedron with eight vertices, twelve edges, and six faces. A vertex in a cube is the point where three edges meet — it's an essential element that gives the cube its shape and structure. In mathematics, a cube is one of the five Platonic solids, which are three-dimensional shapes with identical faces and crystalline symmetry.
Faces
The faces of a shape encompass its flat surfaces, effectively conferring identity and form. For 2D shapes like squares or circles, the term "face" corresponds to the entire shape itself. In 3D shapes, faces are the surfaces enclosed by edges. A cube, for instance, has six faces, each forming one of its sides.
By counting faces, we gain insights into the shape's complexity and dimensionality. Whether it's a simple polygon or a complex polyhedron, the concept of faces is central to grasping a shape's essence.
Edges
Edges are the linear segments connecting vertices, outlining the boundaries of a shape. Edges encapsulate the essence of a shape's outline, providing the framework upon which the shape is built. In 2D shapes, edges are evident as the lines connecting vertices. In contrast, in 3D shapes, they manifest as connecting lines outlining the faces.
For instance, a cylinder boasts two circular faces connected by a curved edge, effectively encompassing its entire structure. Counting edges involves recognizing the lines that define the shape's borders, emphasizing their role in conferring shape and structure.
Whether it's a polygon or polyhedron, all shapes are composed of vertices, faces, and edges that confer structure and form to an otherwise undistinguished mass.
Cylinder Faces, Edges, and Vertices
Like any other shape in a cylinder faces, edges, and vertices also play an integral part. A cylinder lacks vertices, but it possesses two circular faces linked by a curved edge. The number of edges on a cylinder relies on its diameter—a broader cylinder entails more edges compared to a narrower one.
Cylinders hold great significance in geometry as they can shape both regular and irregular forms, such as cones and cylinders themselves. Unlike vertices, which denote the points where multiple lines intersect, cylinders exhibit two faces and an edge that defines their circumference. Their versatility in geometry makes cylinders a valuable tool for crafting various shapes, both regular and irregular.
Meaning of Vertices in Maths
The meaning of vertices in maths is the points where two or more lines intersect. They play an important role in defining the shape of an object — without vertices, shapes would be impossible to define. Mathematicians often use the term "vertex" to refer to any point of intersection—this includes the points at which curves, line segments, and surfaces all meet.
How Many Vertices of a Cone?
If you are puzzled by the question “How Many Vertices of a Cone?”, here is your answer: a cone has one vertex, which is the single point where all its sides converge and intersect, forming a sharp apex. This geometric feature distinguishes a cone from other three-dimensional shapes, adding to its uniqueness and defining its characteristic shape.
The Role of Vertices, Faces, and Edges
Beyond their definitions, vertices faces and edges interact harmoniously to define the essence of geometric shapes. Vertices, interconnected by lines, form the framework on which shapes rest. Edges linear segments connecting these vertices outline boundaries and provide the blueprint for form. Faces, flat surfaces enclosed by edges, bestow presence and identity upon shapes. Some faces are flat, while others embrace curvature, as seen in the contours of a hemisphere.
Exploring Specific Shapes
Beyond basic shapes, our exploration unveils intricate properties of specific geometric forms. Let's examine the tetrahedron—a polyhedron composed of four triangular faces. Its four vertices, six edges, and triangular faces define this multifaceted shape. As we delve further into 3D shapes, we encounter the sphere—a shape that challenges conventional notions of vertices and edges. With no edges and a single curved surface, the sphere demonstrates the diversity of forms that vertices, faces, and edges can assume.
Relevance in Primary School Education
In primary school education, introducing students to geometric concepts is an essential step in their cognitive development. By learning about vertices, faces, and edges, students are able to connect abstract mathematical concepts to real-world applications. This type of engagement with fundamental geometric elements can help to enhance their spatial reasoning and analytical thinking skills, promoting a more well-rounded education.
In fact, by the time students reach Year 2, they are formally introduced to this vocabulary, which serves as a solid foundation for further exploration and understanding of geometry. This highlights the importance of teaching geometric concepts in primary school and its positive impact on a student's overall learning experience.
For instance, a cube is an excellent introduction to 3D shapes. It has six square faces with four vertices at each corner—eight in total. As students gain confidence in recognizing 3D figures, they eventually progress to more complex topics such as pyramids and cones. A pyramid is composed of four triangular faces with one vertex at the peak, while a cone has one circular face and one vertex at its base. By exploring shapes in this manner, children can develop their understanding of vertices, faces, and edges.
Application Across Mathematics
The concept of vertices, faces, and edges is fundamental to various mathematical fields, extending beyond just geometry. In algebraic graph theory, these concepts are represented by nodes, connections, and regions. This representation helps in understanding and studying the properties of graphs.
Additionally, in calculus, the relationship between vertices and edges is crucial in explaining surface integrals, a key concept in mathematical analysis. Therefore, a thorough understanding of vertices, faces, and edges is essential for anyone pursuing mathematics.
Geometry and the Digital Age
The world of computer graphics relies on vertices, edges, and faces to construct 3D models that simulate reality. Video games, architectural renderings, and virtual reality experiences all depend on the meticulous arrangement of these geometric elements. The precise coordination of vertices and edges gives rise to the intricate structures that immerse us in virtual worlds, demonstrating the tangible impact of abstract mathematical concepts.
Vertices, Faces, and Edges in Everyday Life
In the midst of complex abstract concepts, it is crucial to recognize the practical significance of vertices, faces, and edges in our everyday lives. From the solid structures that provide us shelter to the intricate jewelry designs we wear, these geometric fundamentals are present all around us. Engineering marvels like suspension bridges boast vertices at their towers, edges of cables, and faces of roadway decks.
The shapes of buildings, the precision of gadgets, and the aesthetic appeal of various objects all reflect the influence of mathematical craftsmanship. By acknowledging the widespread presence of geometry, we cultivate a deeper understanding of the interconnections between knowledge and its tangible expressions.
MathMaster - Math Solving Tool
If you are stuck with vertices, faces, and edges, then MathMaster is the right tool for you. MathMaster is an innovative math app that helps students solve their mathematical problems in a jiffy. It provides ready-made solutions to numerous topics like geometry, algebra, and calculus; all at the touch of a button. The intuitive UI makes the app easy to use, and its step-by-step guidance eliminates any confusion.
Conclusion
Understanding the concept of vertices, faces, and edges is crucial in geometry. When considering the vertex of a cube, it is important to note that a cube has 8 vertices. On the other hand, when discussing the cylinder, it does not have any vertices. The meaning of vertices in maths refers to the meeting points of two or more lines or edges. Furthermore, for how many vertices of a cone, there is only one vertex. Lastly, we discussed cylinder vertices. Well, they do not have any vertices but are instead characterized by their curved surface.
By understanding these definitions and quantities of vertices, we can delve deeper into the geometric fundamentals of these shapes.
Just as the vertex of the cube marks a singular point of convergence and the presence of cylinder vertices highlights essential structural junctures, these concepts unite to form the essence of shape, structure, and form.