What Is Mean Average?

When it comes to mathematics, one concept that frequently arises is the idea of an average. The term "average" is used extensively in various fields of mathematics, from statistics to everyday calculations. This article will delve into what is average in maths, exploring its definition, calculation, and practical applications.

What Is Average In Maths?

The mean average, often simply referred to as the average, is a fundamental mathematical concept used to summarize a set of numbers. It provides us with a single value representing the entire dataset's typical value. In other words, the mean definition in maths is the value around which all the numbers in the dataset tend to cluster. The mean is essentially the sum of all the numbers divided by the total count of numbers.

Calculation of Mean Average

Calculating the mean average involves a straightforward process:

1. Add Up the Numbers: Begin by adding up all the numbers in the dataset. For instance, if you have the numbers 5, 10, 15, 20, and 25, the sum would be 75.
2. Count the Numbers: Determine the total count of numbers in the dataset. In the example above, there are five numbers.
3. Divide to Find Mean: Divide the sum of the numbers by the total count of numbers. In our example, 75 divided by 5 equals 15.

The formula for calculating the mean average can be represented as follows:

Mean average = Sum of numbers/Total count of numbers

Practical Example (Mean Average)

To illustrate the concept further, let's consider a practical example to understand the meaning of mean in math. Imagine you have a class of students, and you want to find the mean average of their test scores:

Student	Test Score
Alice	85
Bob	92
Carol	78
David	65
Emily	88

1. Sum of Scores: 85 + 92 + 78 + 65 + 88 = 408
2. Total Count: There are five students.
3. Mean Average: 40/85 = 81.6

Hence, the mean average test score in this class is 81.6.

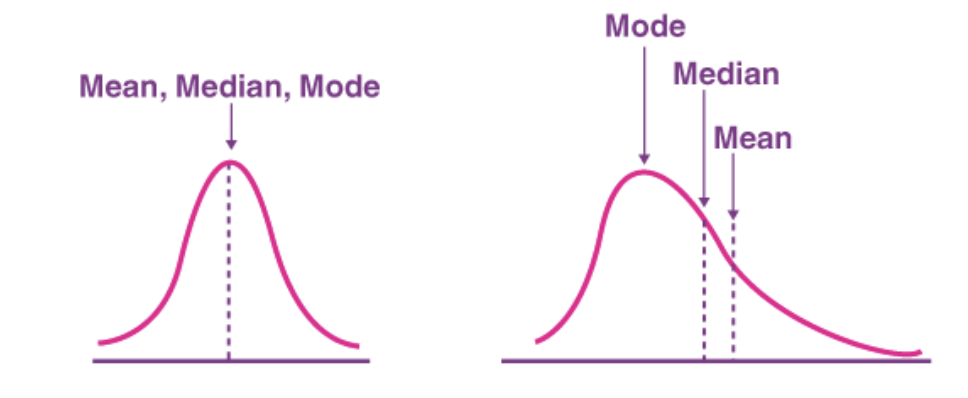
Key Properties of Mean Average

The mean average has several important properties that make it a valuable statistical tool:

1. Balancing Effect: The mean balances out extreme values in a dataset. Unusually high or low values have less impact on the mean compared to other ways we look at groups of numbers.
2. Sensitive to Changes: The mean is sensitive to any changes in the dataset. A slight alteration in any number can affect what is average in maths.
3. Arithmetic Center: Think of the mean as the arithmetic center of the dataset. It's the point around which the numbers "balance." This is ultimately the meaning of mean in math.

How does mean average relate to other areas of math?

The mean average's impact spans diverse mathematical fields. It's a fundamental measure in statistics, calculus, and probability theory, aiding data analysis, outcome prediction, and modeling. In linear algebra, it's integral for understanding vectors, matrices, and eigenvalues. Mean values underpin economic indicators and geometrical centers while also influencing physics, aiding in comprehending wave amplitudes and particle behavior, highlighting the mean definition in maths. This concept unifies math disciplines, threading through statistics, calculus, linear algebra, economics, and physics, highlighting its essential role.

MathMaster Helps Find The Mean Average The Easy Way

Finding what is average in maths questions is not always easy. You may be facing difficulties while calculating, so it is likely time to consider using the math-solving tool MathMaster. MathMaster is designed to assist you in solving various mathematical problems, including those related to averages and other fundamental concepts. No matter if you're a student or someone who uses math at work, MathMaster can be your special helper to get better at math and learn more about it.

Conclusion

The mean definition in maths can be highlighted as a crucial mathematical concept used to summarize and understand datasets. We can find the central value around which the data clusters by calculating the mean. This simple yet powerful concept applies in various fields and can provide valuable insights into various scenarios. Remember, whether you're dealing with test scores, income data, or any other numerical information, the mean average can help you make sense of the numbers.

FAQs

Does the mean average always have to be a whole number?

No, the mean average can actually be a decimal or a fraction, even if the original numbers are all whole numbers. This can happen when the sum of the numbers doesn't divide evenly by the total count. So, don't be surprised if the mean turns out to be something like 2.5 or 3/4.

Why is the mean sometimes not a good representation of the dataset?

The mean average, as you know, seeks to capture the central tendency of a dataset by summing up all the numbers and dividing by their count. However, the presence of outliers, those data points that substantially deviate from the norm, can significantly impact the accuracy of the mean's representation. To illustrate, consider an examination where most students perform well, yet a single student garners a perfect score. The exceptional score has the potential to exert an undue influence on the mean, erroneously suggesting that the entire cohort excelled similarly. In such instances, alternative measures of central tendency like the "median" or the "mode" prove invaluable in providing a more accurate portrayal of the data distribution.

Is the mean average the only way to find the "average" of a group of numbers?

No, there are other types of averages, too. The mean average is the sum of all numbers divided by how many there are. The median, on the other hand, is the middle number when the numbers are in order. And the mode is the number that appears the most. Each of these averages gives us a different perspective on the data.

Can you give an example of how the mean average is used in everyday situations?

Imagine you're a teacher and want to know how well your class did on a test. Finding the mean average of their scores gives you a sense of how the class, as a whole, performed. It helps you understand the overall performance without getting swayed by really high or really low scores.