MathMaster Blog

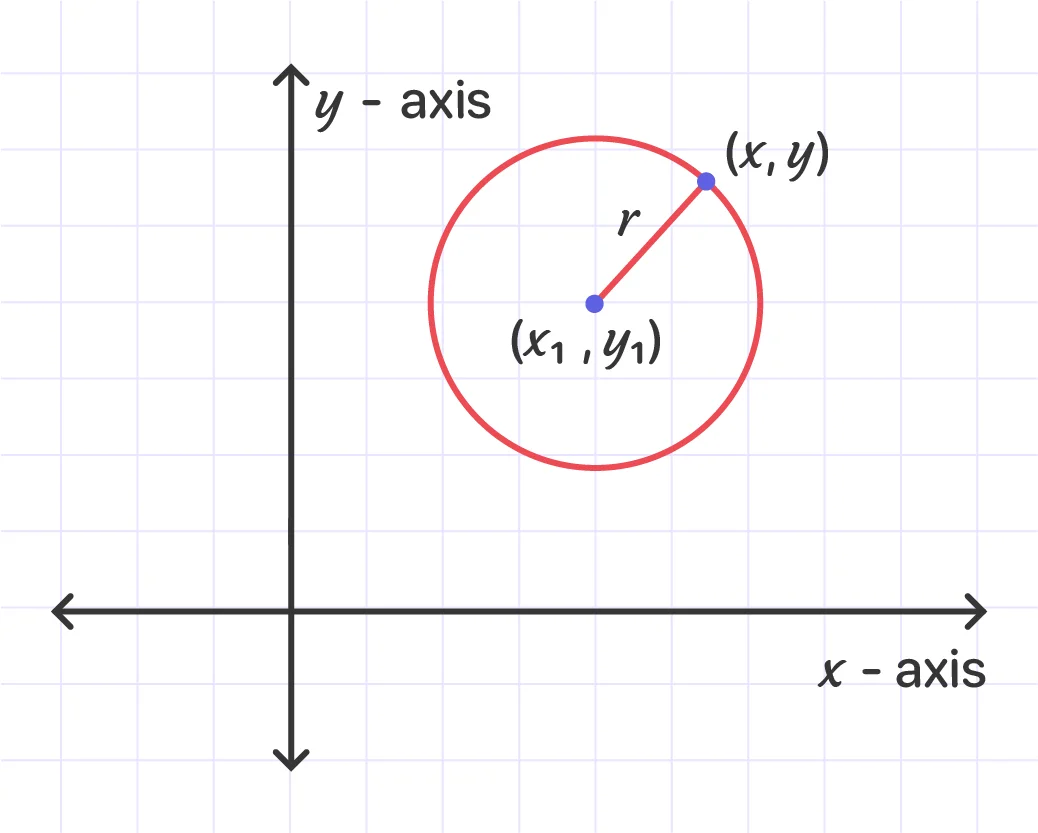
The equation of a circle can be found using the center and radius. It represents all the points that lie on the circumference of the circle.

The equation of a circle formula is:

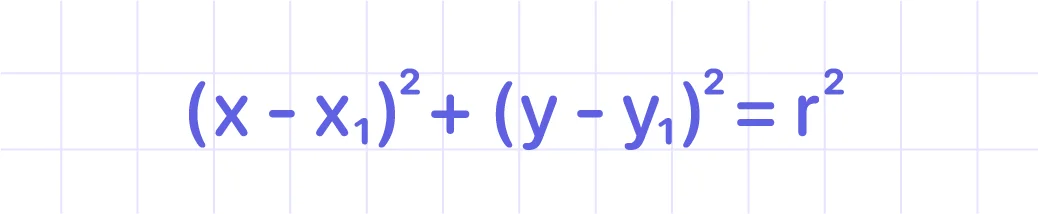
where (x1,y1) is the center of the circle with radius r and (x, y) is an arbitrary point on the circumference of the circle?

Example 1:

Find the equation of the circle in standard form for a circle with center (2, -3) and radius 3.

Solution:

In standard form, the equation for a circle is (x - x1)^2 + (y - y1)^2 = r^2.

Here, (x1, y1) = (2; -3) is the center of the circle. Radius is 3.

(x - 2)^2 + (y - (-3))^2 = (3)^2

(x - 2)^2 + (y +3)^2 = 9

Answer: (x - 2)^2 + (y +3)^2 = 9 is the required standard form of the equation of the given circle.

Example 2:

Find the equation of the circle with center (2; -3) and radius $\sqrt{7}$.

Solution:

(x - 2)^2 + (y -(-3))^2 = ($\sqrt{7}$)^2

(x - 2)^2 + (y +3)^2 = 7

Example 3:

Which of the following points does NOT lie on a circle centered at (3, 0) with a radius of 3?

a)(-3, 0)

b)(6, 0)

c)(3, 3)

d)(0, 0)

e)(3, -3)

Solution:

For a circle centered at (3,0) with a radius of 3, the equation is

(x - 3)^2 + y^2 = 9.

Putting -3 instead of x and 0 instead of y, we have:

(-3 - 3)^2 + (0)^2 = (-6)^2= 36 ≠ 9.

Answer: a) (-3, 0) does not lie on the circle.

Example 4:

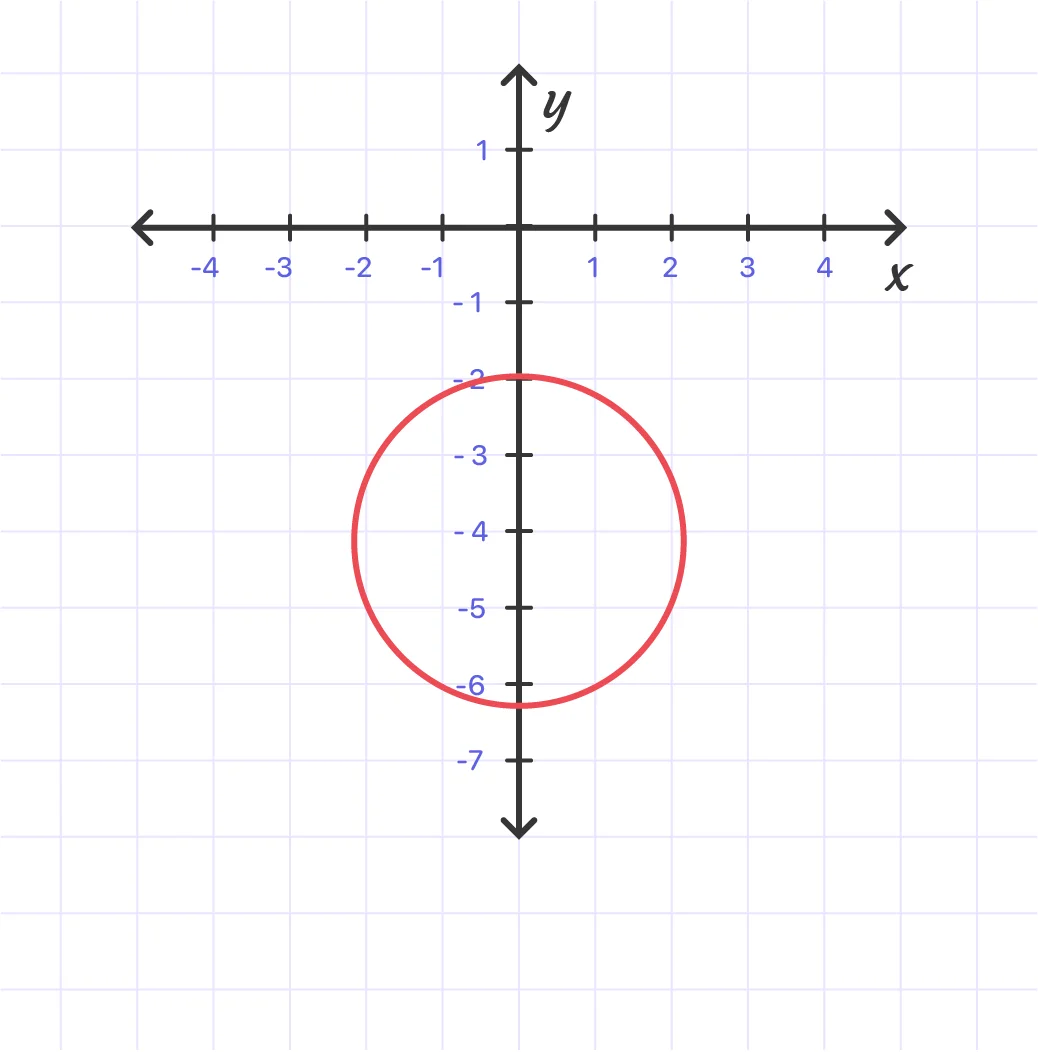
The standard form of the equation of a circle is (x -h)^2 + (y - k)^2= r^2, where (h, k) is the center of the circle and r is the radius.

Thus, h = 0, k = -4, r = 2.

The standard form is x^2 + (y + 4)^2 = 4.

The general form can be found by moving everything to the left side and expanding:

x^2 + y^2 + 8y + 12 = 0

So, the diameter is d = 2r = 4

Circumference: C = 2πr = 4π

Area: A = πr^2 = 4π