MathMaster Blog

When the leading coefficient or the sign of 'a' is negative, the quadratic function f(x) = aх^2 + bx + c will have its maximum value. When a is negative, the quadratic function graph is a parabola that opens downward.

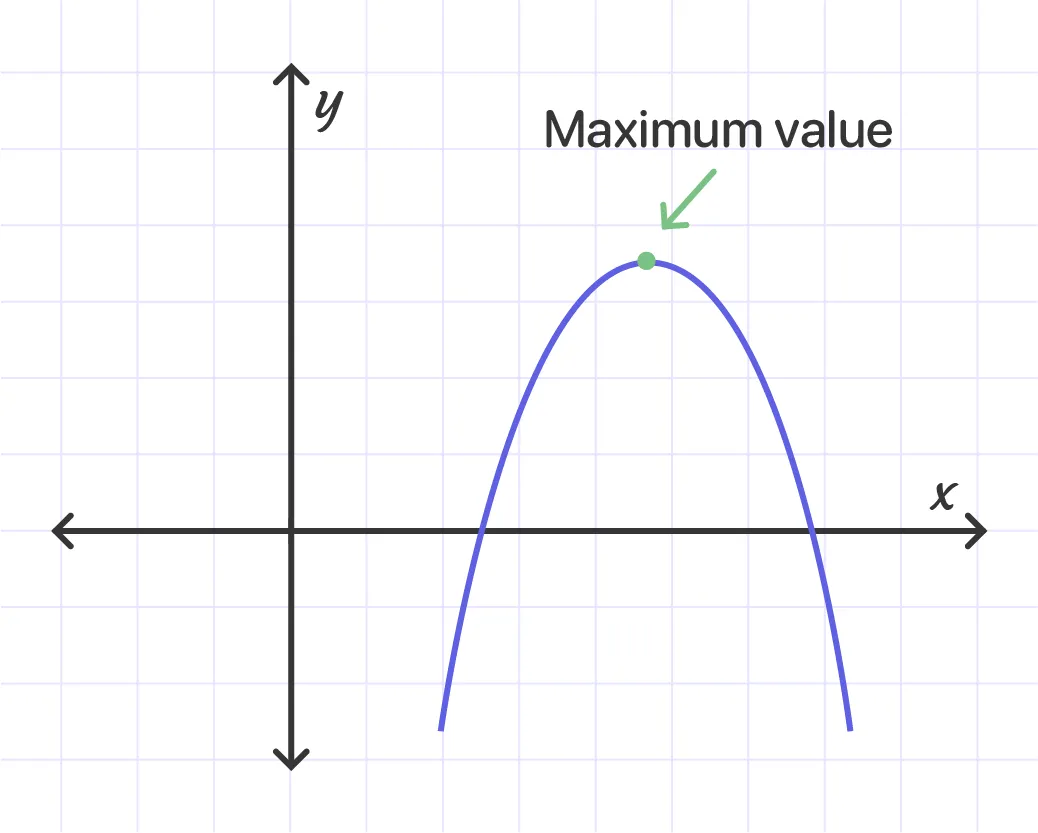
The maximum value is y coordinate at the vertex of the parabola. Note that there is no minimum value for the parabola which opens down.

The quadratic function f(x) = aх^2 + bx + c will have the minimum value when the leading coefficient or the sign of a is positive. The graph of the quadratic function will be a parabola that opens up when a is positive.

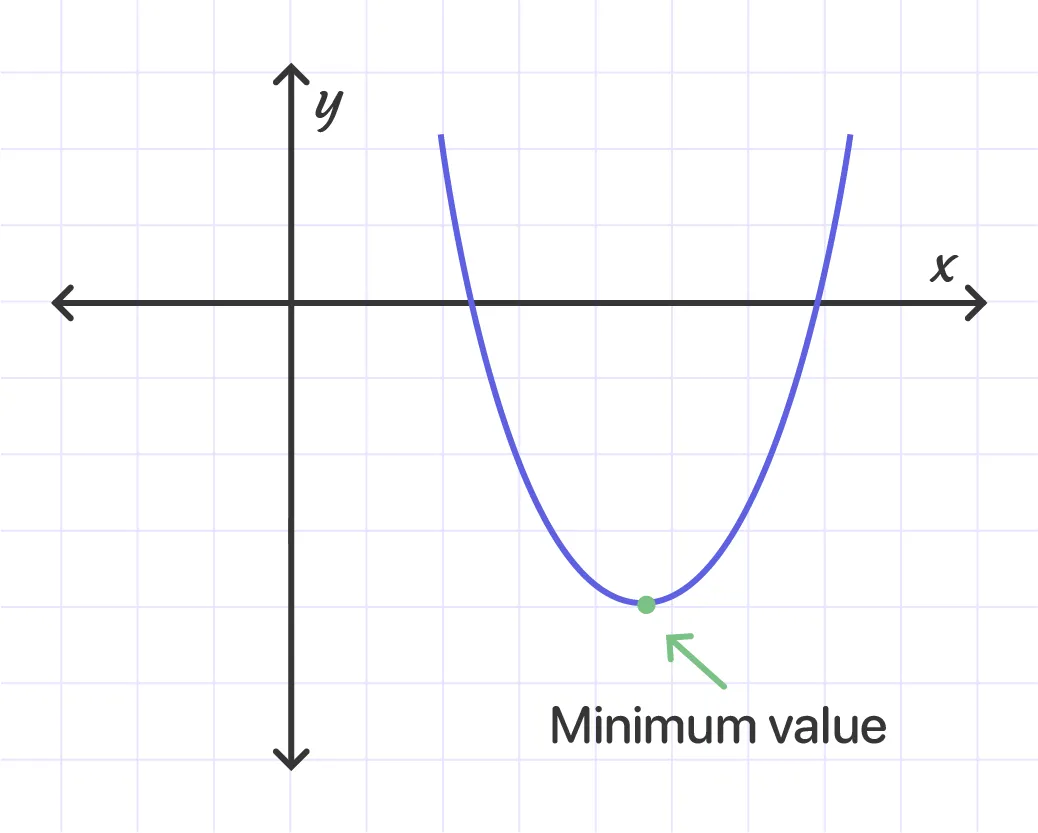
The minimum value is y coordinate at the vertex of the parabola. Note that there’s no maximum value for the parabola which opens up.

Example:

Find the minimum or maximum value of f(x) = 2х^2 + 7x + 5.

Solution:

The parabola is open upward because the coefficient of х2 is positive. Therefore, the function will only have the minimum value, which is the vertex y-coordinate.

First, we have to find the x-coordinate of the vertex to evaluate the y-coordinate. For this, we should use the formula -b/2a.

Then, substitute a with 2 and b with 7.

So, $x = -\frac{b}{2a} = -\frac{7}{4}$

To find the y-coordinate of the vertex, substitute -7/4 for x.

So, y-coordinate is:

= f(-7/4)

= 2(-7/4)2 + 7(-7/4) + 5

= 2(49/16) - (49/4) + 5

= (49/8) - (49/4) + 5

= (49 - 98 + 40)/8

= -9/8

Answer: The minimum value is -9/8. There is no maximum value for this function.