MathMaster Blog

The space occupied by a parallelepiped in a three-dimensional plane is defined as its volume. It is expressed in cubic units, like in^3, cm^3, m^3, ft^3, yd^3, etc. The formula for the volume of a parallelepiped is given by:

To calculate the volume of a parallelepiped from its sides (or edge lengths), use the formula:

V = a x b x c x √(1 + 2 x cos(α) x cos(β) x cos(γ) - cos²(α) - cos²(β) - cos²(γ))

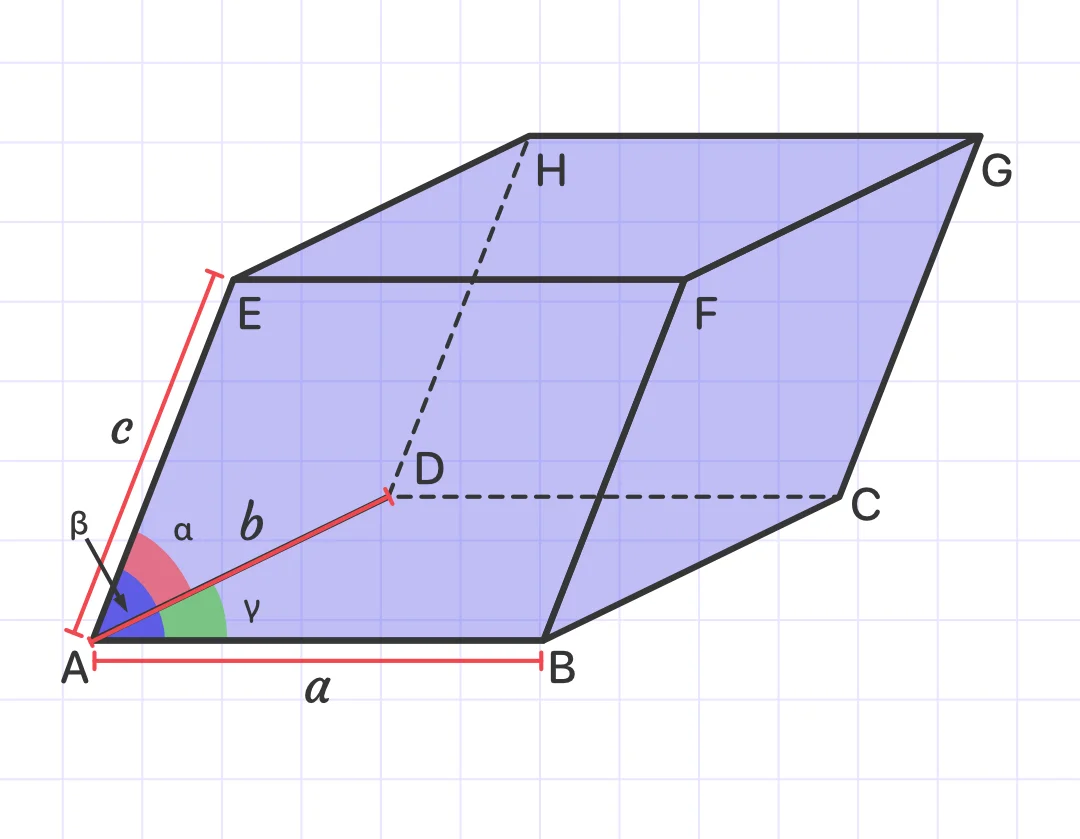
Example 1:

Determine the volume of the parallelepiped based on the vectors:

Solution:

Step 1:

Take the cross product of b and c.

Step 2:

Take the dot product of

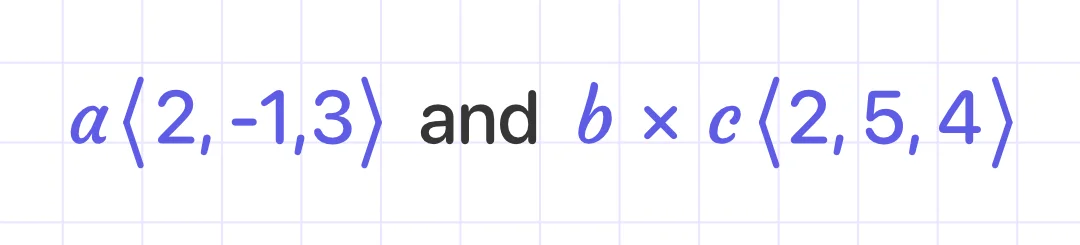
Answer: The volume of the parallelepiped is 11.

Example 2:

A rectangular box has a volume of 10x^2 and a length of 3x and a width of 2x. What is the height of the box?

Solution:

Input the volume, length, and width into the following formula to get the volume of a box:

V = l x ω x h

10x^2 = (2x)(3x)h

10x^2 = 6x^2h

Then, divide both sides by 6x^2:

10/6 = h(5/3) = h

Answer: The height of the box is 5/3.