MathMaster Blog
A radical function is made up of a radical expression with the independent variable as the radicand. Radical functions require you to consider the domain of the function before you graph it. The domain is the x values of a given function or relation.
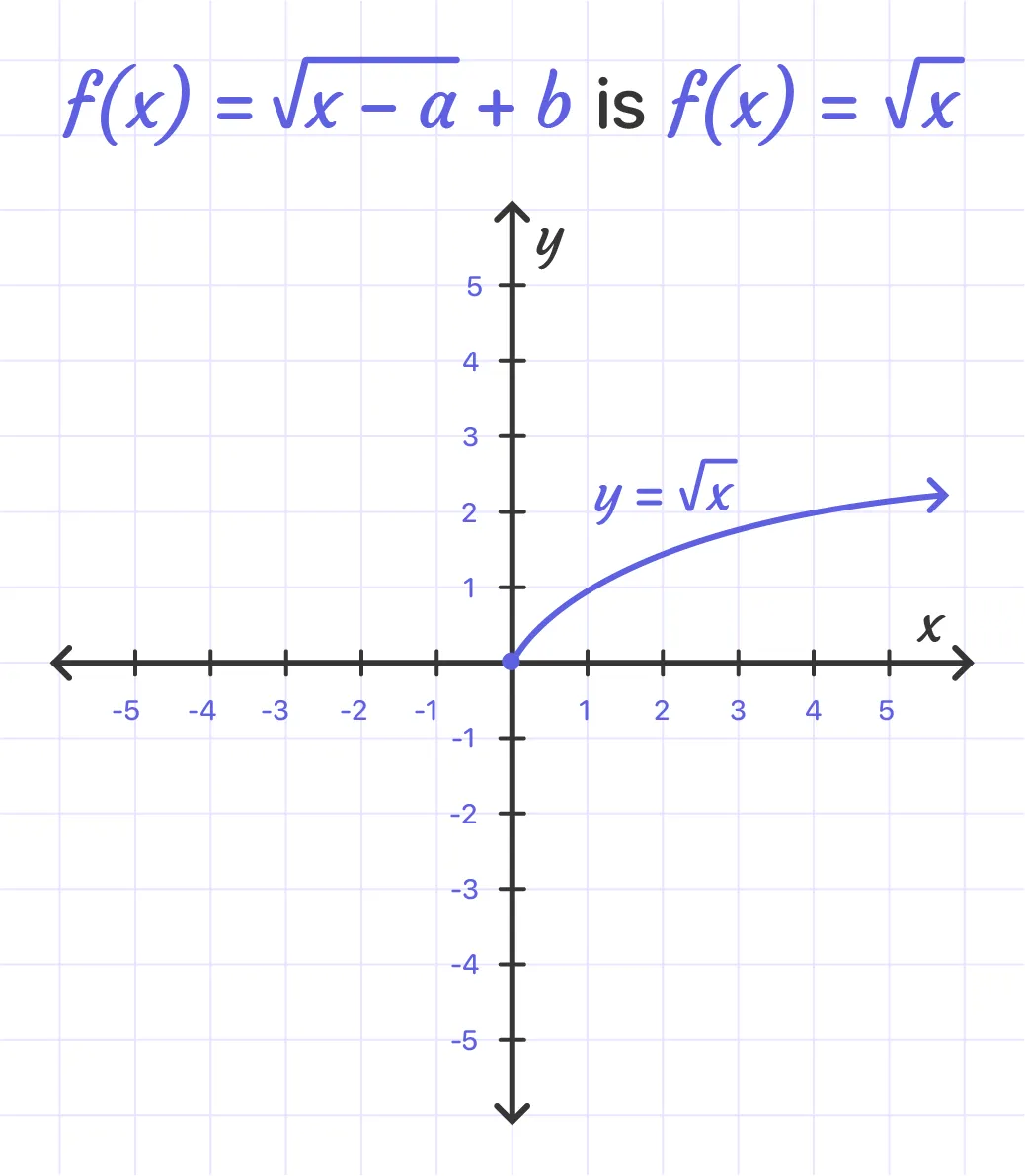
The graph of f(x) = $\sqrt{x- a} + b$ can be obtained by translating the graph of f(x) = $\sqrt{x}$ to A units to the right and then B units up.
Example 1:
Graph the function f(x) = $\sqrt{x- 1} + 2$ from its parent graph y = $\sqrt{x}$.
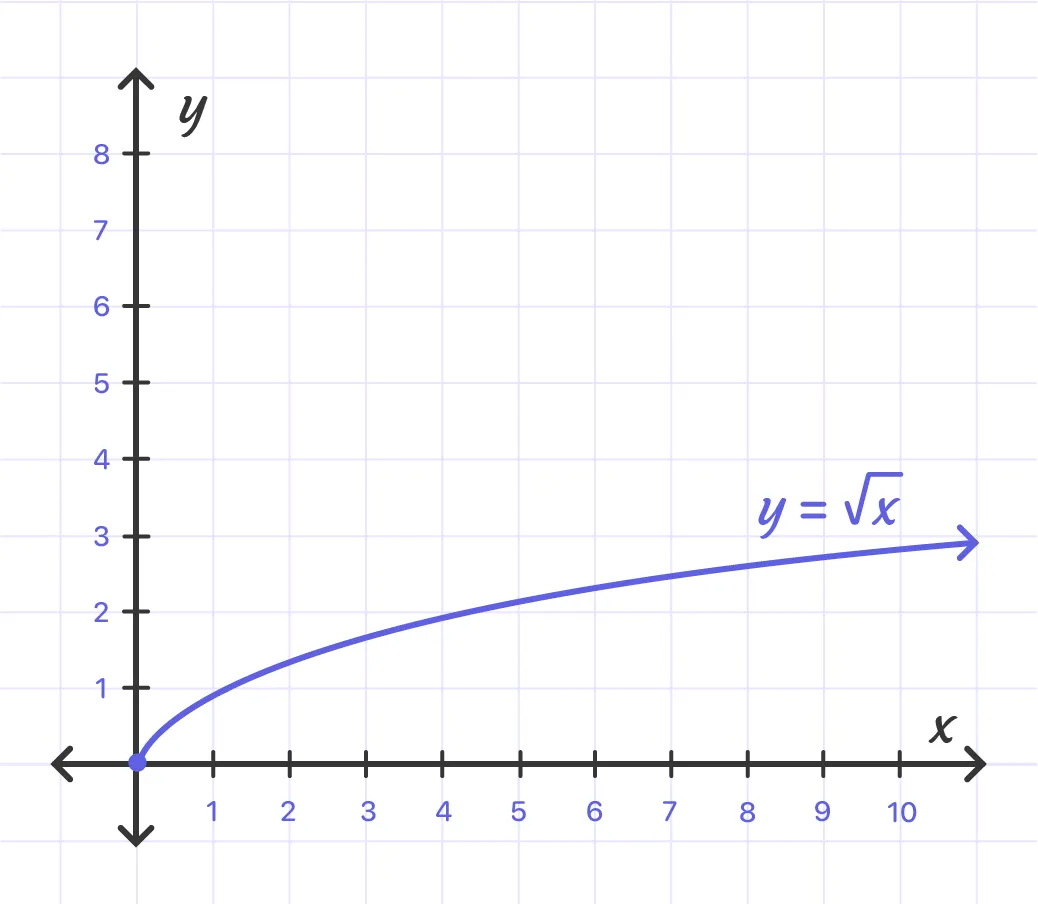
Step1:
Plot the graph for y = $\sqrt{x}$.
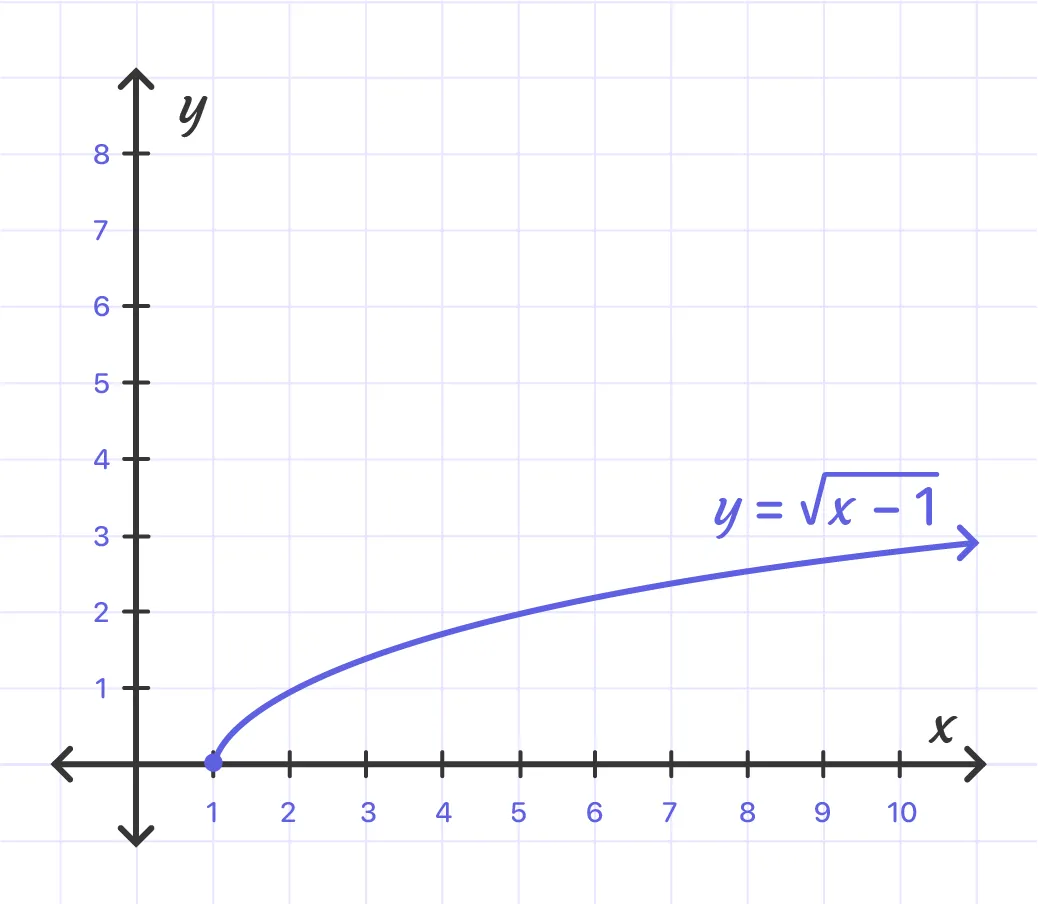
Step2:
Move the graph by 1 unit to plot the y = $\sqrt{x- 1}$. Then move the graph by 2 units up to draw $\sqrt{x- 1} + 2$.
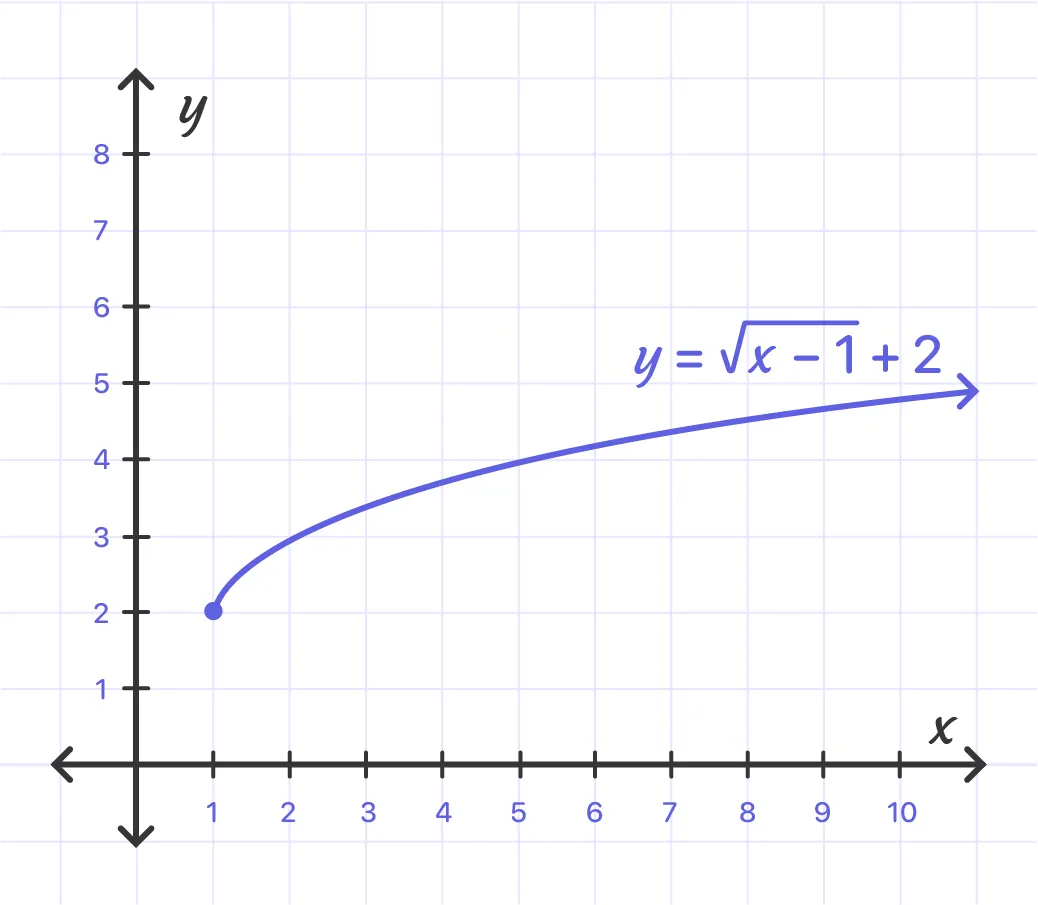
The domain of the function
y = $\sqrt{x- 1} + 2$ is ≥ 1.
The range of the function
y = $\sqrt{x- 1} + 2$ is ≥ 2.
Example 2:
What is the domain of the function
y = $\sqrt{x^2 - 10}$?
Solution:
$x^2$ - 10 ≥ 0
= $x^2$ ≥ 10
-$\sqrt{10}$ and $\sqrt{10}$ are the critical points.
Test x = 0 to see that the interval between -$\sqrt{10}$ and $\sqrt{10}$ doesn’t satisfy the equation.
Answer: The domain of the function f(x) = $\sqrt{x^2 - 10}$ is x ≥ 10 and x ≤ -10.