Similarity of triangles

Figures that are congruent have the same shape and dimension.

Similar figures, on the other hand, are identical in form but vary in size.

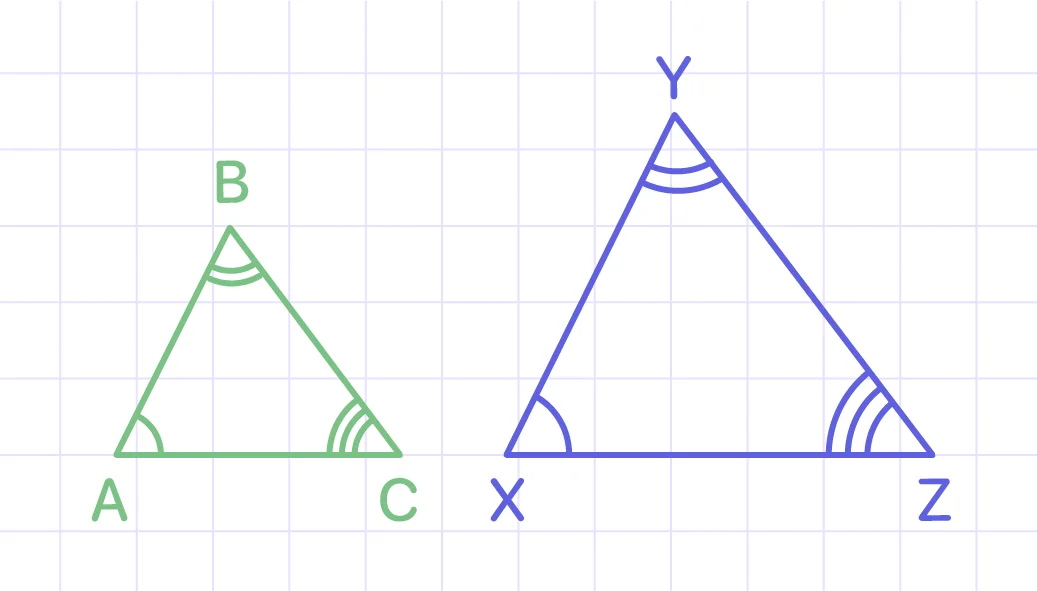
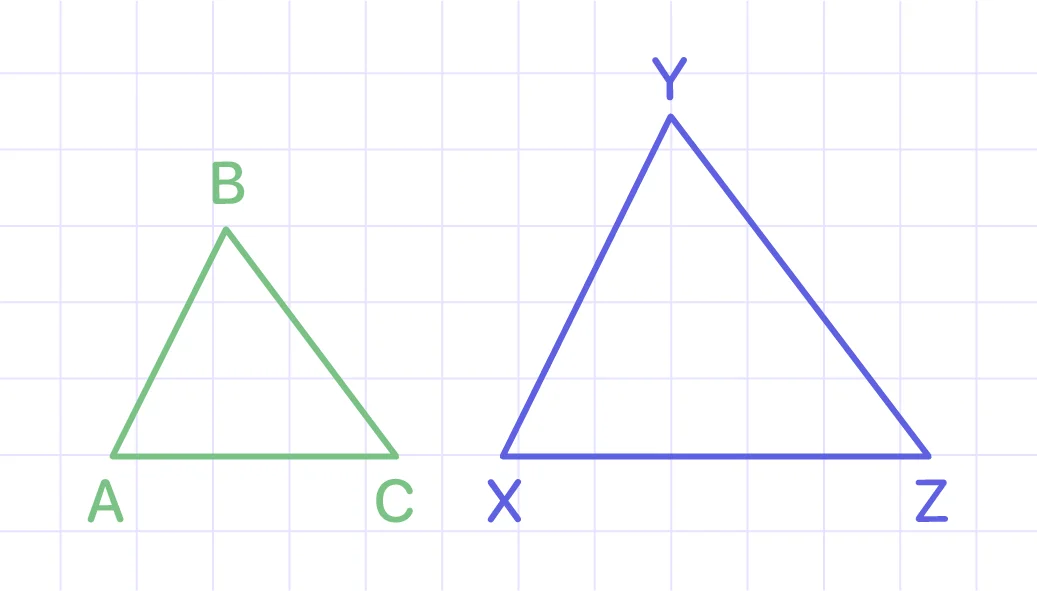
According to the picture, triangles ABC and XYZ are similar, but not congruent; they have the same angle measures, but not the same side lengths.

If two triangles meet one of the following requirements, they are similar:

Angle-angle: Two pairs of corresponding angles are equal.

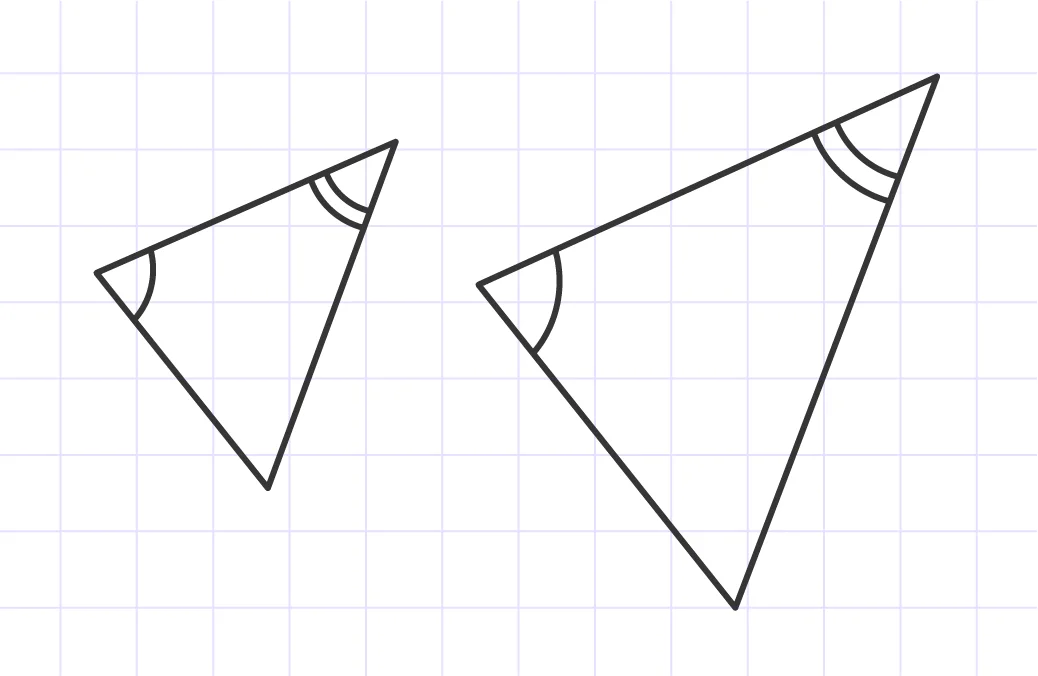
Side-side-side: Three pairs of corresponding sides are proportional.

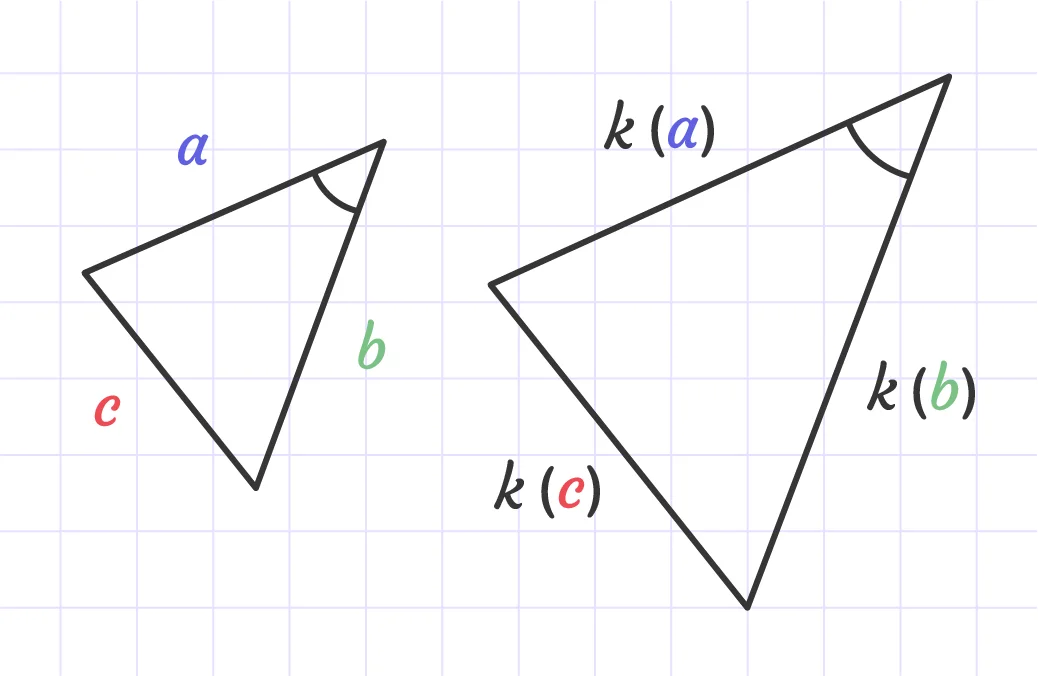
Side-angle-side: Two pairs of corresponding sides are proportional and the corresponding angles between them are equal.

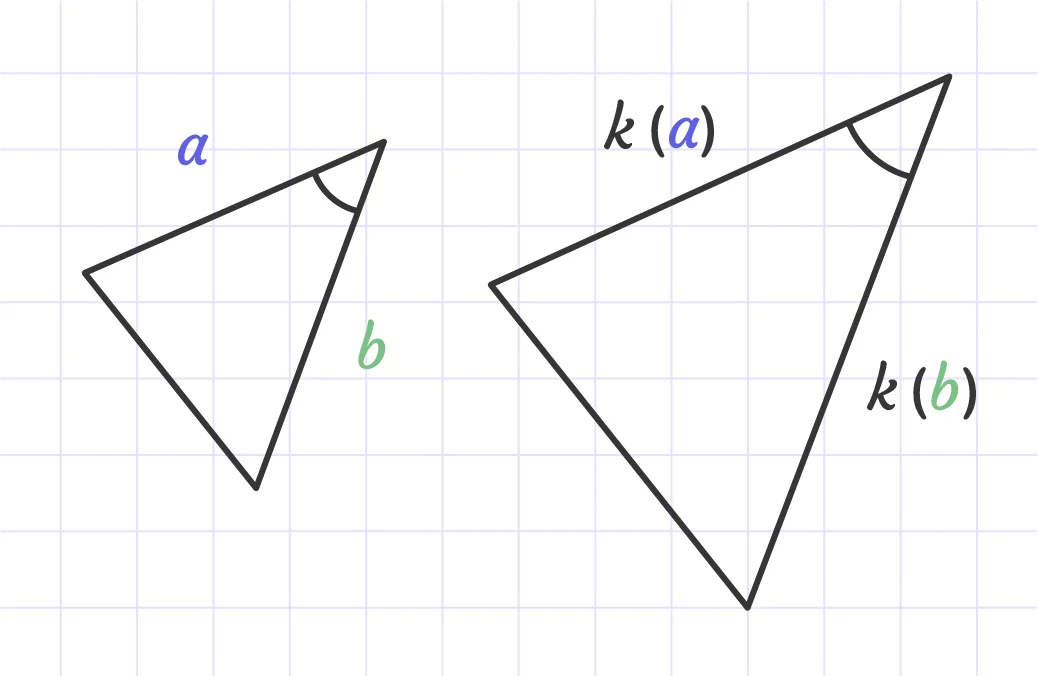
To find the missing side length, we should:

• Step 1: Use two pairs of corresponding sides to write a proportionate relationship.
• Step 2: Plug in known side lengths.
• Step 3: Solve the proportion.

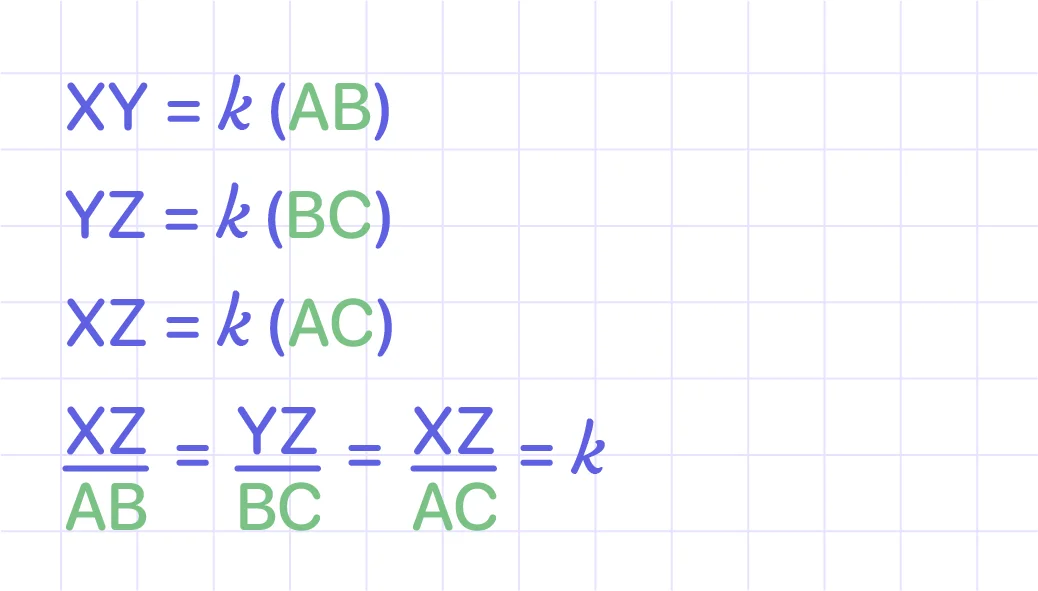
Example 1:

Set up a proportion and use it to solve for x.

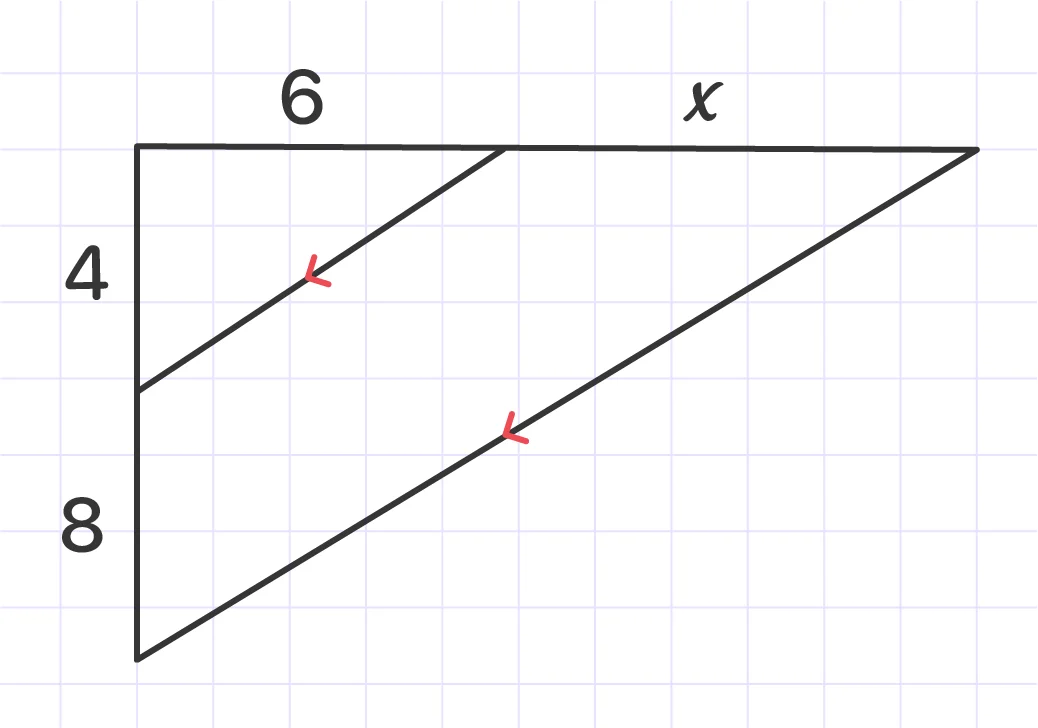
8/4 = x/6

4x = 6 x 8

4x = 48

Answer: x = 12

Example 2:

There are two triangles: ABC and A’B’C’. If ∠А = ∠А’, ∠B = B’, and ∠C = ∠C’, then the triangles are:

a)congruent

b)similar

c)regular

d)equilateral

e)isosceles

Solution:

Two triangles are similar if the corresponding angles are equal.

Answer: B