MathMaster Blog
The standard form of a quadratic equation is $ax^2+ bx + c = 0$, where a, b, and c are constants and x is the variable. Solutions of the equation are the values of x that fulfill the equation, therefore a quadratic equation can only have two solutions.
Methods for solving quadratic equations:
- Factorizing of Quadratic Equation
- Formula Method of Finding Roots
- Completing the Square
- Graphing
The Quadratic Formula is the most straightforward method for determining the roots of a quadratic equation. The roots of the quadratic equation help to find the sum and product of the roots.
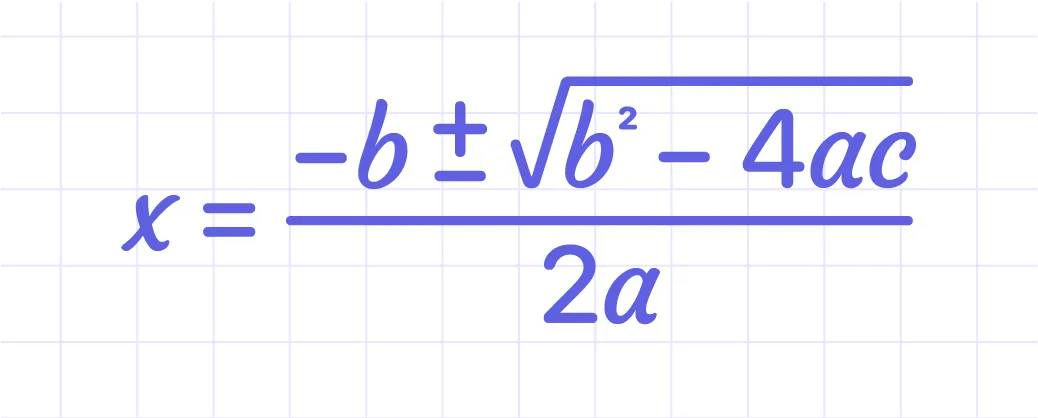
The ± means there are TWO answers:
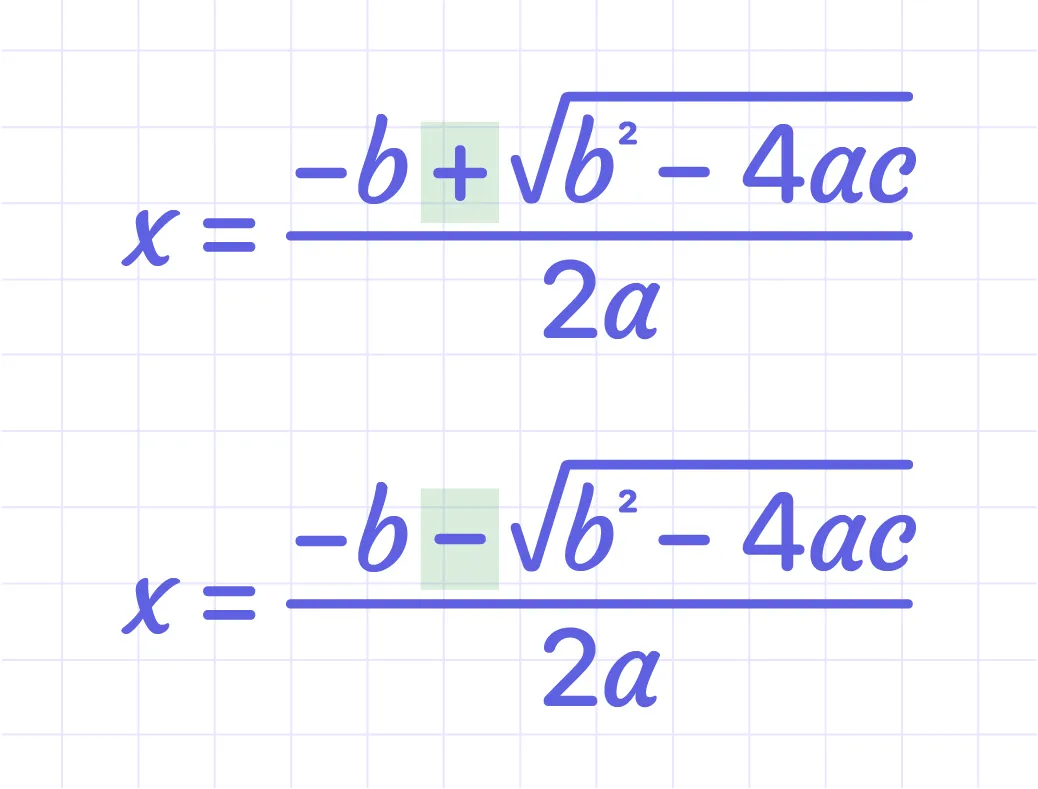
Factoring quadratics is a way to express the quadratic equation $ax^2+ bx + c = 0$ as a product of its linear factors as (x - k)(x - h), where h and k are the quadratic equation's roots. In other words, factoring a quadratic means finding what to multiply to get the quadratic.
Example:
Solving quadratic equation using the formula method of finding roots.
$5x^2 + 6x + 1 = 0$.
To solve this equation, put coefficients in the quadratic formula.
$x = \frac{-6 \pm \sqrt{6^2 - 4 \times 5 \times 1}}{2 \times 5}$
$x = \frac{-6 \pm \sqrt{36 - 20}}{10}$
$x = \frac{-6 \pm \sqrt{16}}{10}$
$x = \frac{-6 \pm 4}{10}$
x = -0.2 or x = -1
Answer: x = −0,2 or x = −1
Example:
Solving quadratic equation by factoring.
$x^2 - 3x - 10 = 0$
Factor the equation. For this, use the sum-product pattern:
If we find two numbers a and b such that
a + b = -3, a x b = -10,
then x2- 3x - 10 = (x + a)(x + b)
We may get the numbers we need by considering the pairs of integers whose product is -10 and then eliminating those whose total isn't -3. The values we require are a = 2 and b = -5.
Therefore, the factored expression is (x + 2)(x - 5).