MathMaster Blog

The whole point of the interval method is to determine the intervals of the values of the variable, where the situation does not change, and then to consider them as a whole.

Example:

Solve $x^2-5x+6 ≥ 0$.

First, let's factorize the square trinomial.

$x^2-5x+6 = 0$

$D = 5^2-4*1*6 = 25-24 = 1$

$x_{1,2} = \frac{-5 \pm \sqrt{1}}{2}$

$x_{1} = 3; x_{2} = 2$

$x^2-5x+6 = (x - 3)(x- 2)$

So, now we have (х - 3)(х - 2) ≥ 0.

Secondly, let's analyze two factors:

The first one: x - 3. This factor can change sign at x = 3, which means that for x < 0 this expression is negative: x - 3 < 0, and for x > 0 it takes positive values: x - 3 > 0.

The second one: x - 2. For this factor, such a "sign" point: x = 2.

Conclusion: the sign of the equation (x - 3)(x - 2) changes only when the variable passes through the values x = 3 and x = 2.

Now, let’s draw a number line:

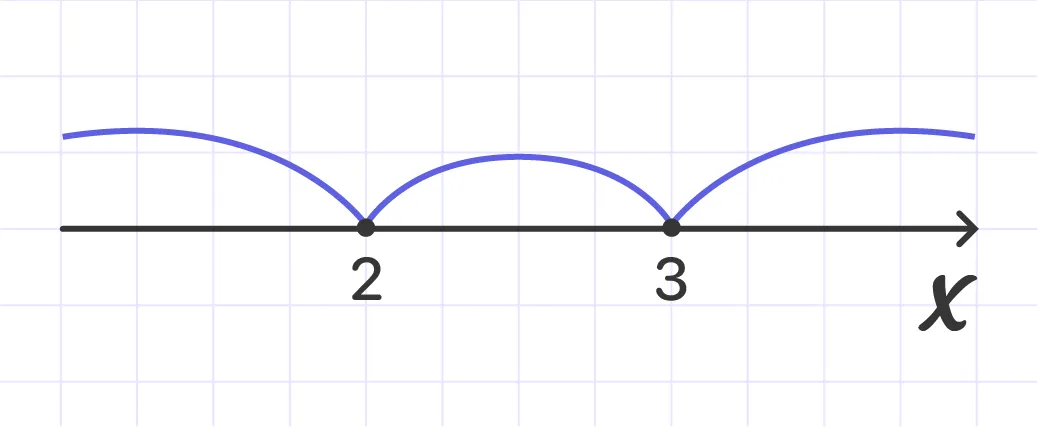
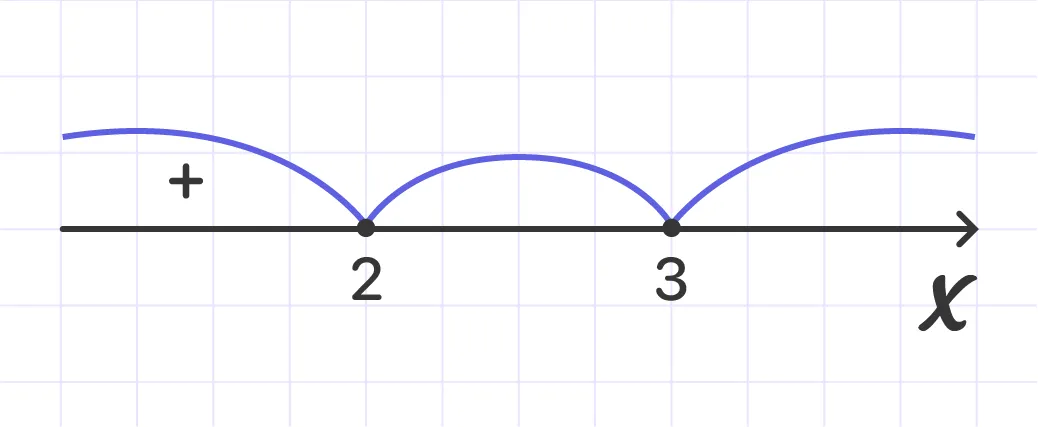
Consider the intervals from left to right. x < 0 - the situation does not change on this interval, which means that to determine the situation, you can take any value from this interval and substitute it into the equation.

For instance, x = -1. Now, let’s substitute:

(-1 - 3)(-1 - 2) = -4(-3) = 12

12 > 0

Conclusion: for x < 0, the inequality (x - 3)(x - 2) > 0 is true. Have a look:

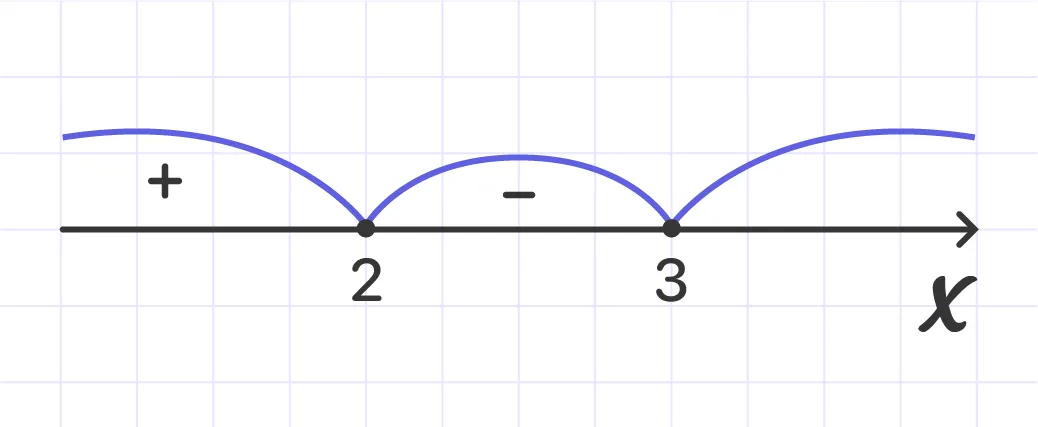
2 < x < 3 - the situation does not change on this interval, which means that in order to determine the situation, you need to take any value from this interval and substitute it into the equation.

For example: x = 2.5. Now, let’s substitute:

(2.5 - 3) (2.5 - 2) = -0.5 х 0.5 = - 0.25 < 0

Conclusion: for 2 < x < 3, the inequality (x - 3) * (x - 2) < 0 is true. Have a look:

х > 3 — the situation does not change on this interval. So you need to take any value from this interval and substitute it into the product.

For example: x = 25.

(25 - 3) (25 - 2) = 22 х 23 = 506 > 0

Conclusion: for x > 3, the inequality (x - 3)(x - 2) > 0 is true. Have a look:

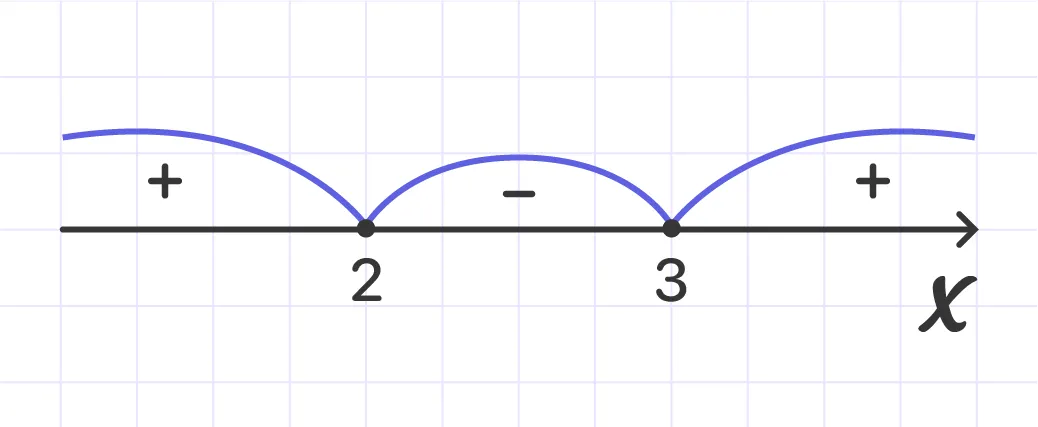
Initial inequality: (x - 3)(x - 2) ≥ 0.

Now, let’s color the points that satisfy the inequality, and leave the points that don't.

Answer: х ≤ 0, х ≥ 3