MathMaster Blog

A radical equation is one in which one of the variables is under a radical.

To resolve a radical equation, do the following:

Step 1: Isolate the radical expression involving the variable. If more than one radical expression involves the variable, then isolate one of them.
Step 2: Raise both sides of the equation to the index of the radical.
Step 3: If there is still a radical equation, repeat steps 1 and 2; otherwise, solve the resulting equation.
Step 4: Check the answer in the original equation.

Example:

Solve $\sqrt{3x^2 + 10x} - 5 = 0$.

Step1:

Isolate the radical part

$\sqrt{3x^2 + 10x} = 5$

Step2:

Raise both sides to the index of the radical and square both sides.

$Solving radical equations step 2$

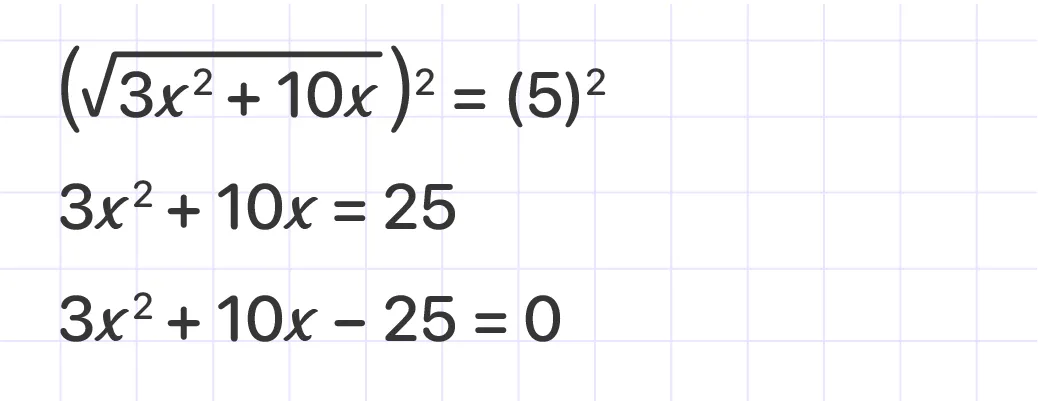
Step3:

Apply the quadratic formula:

$Solving radical equations step 3$

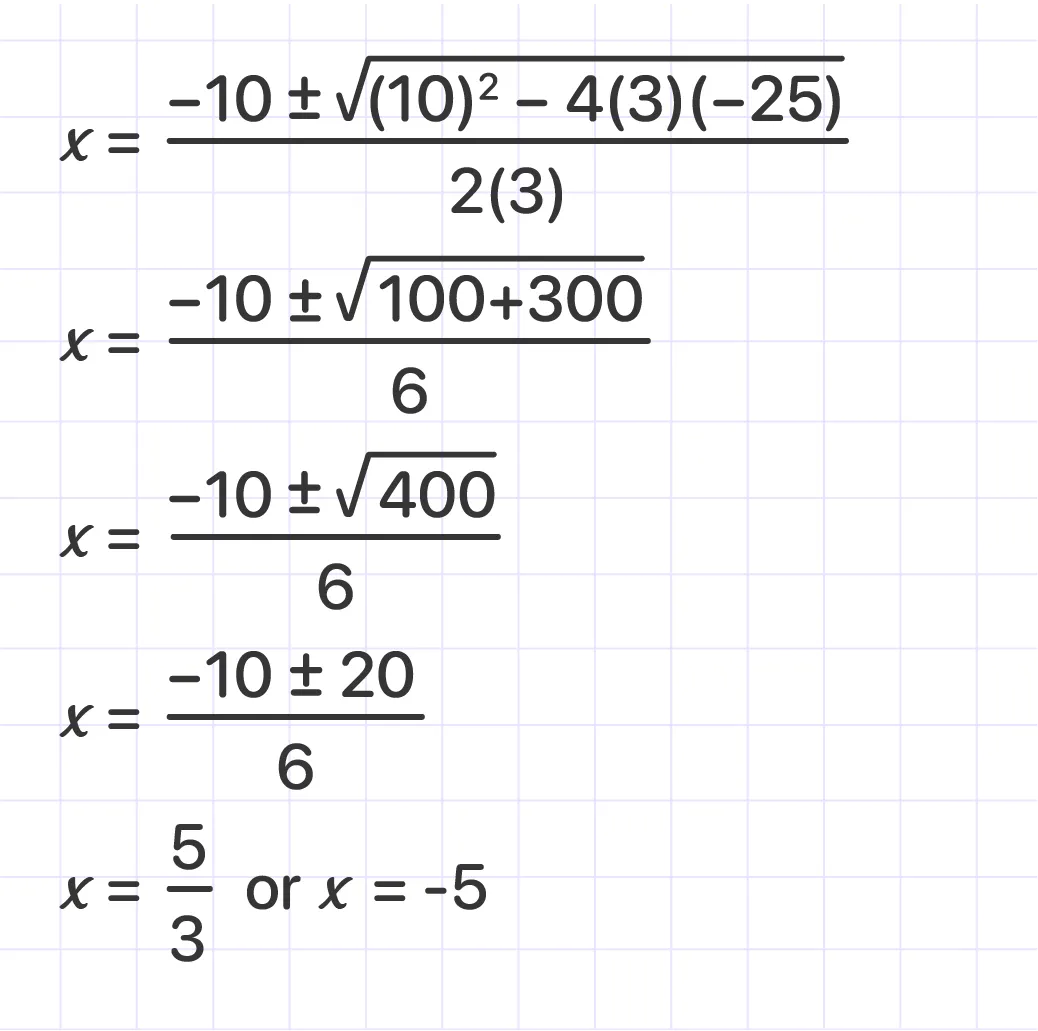
Step4:

Check the result:

$Check the result$

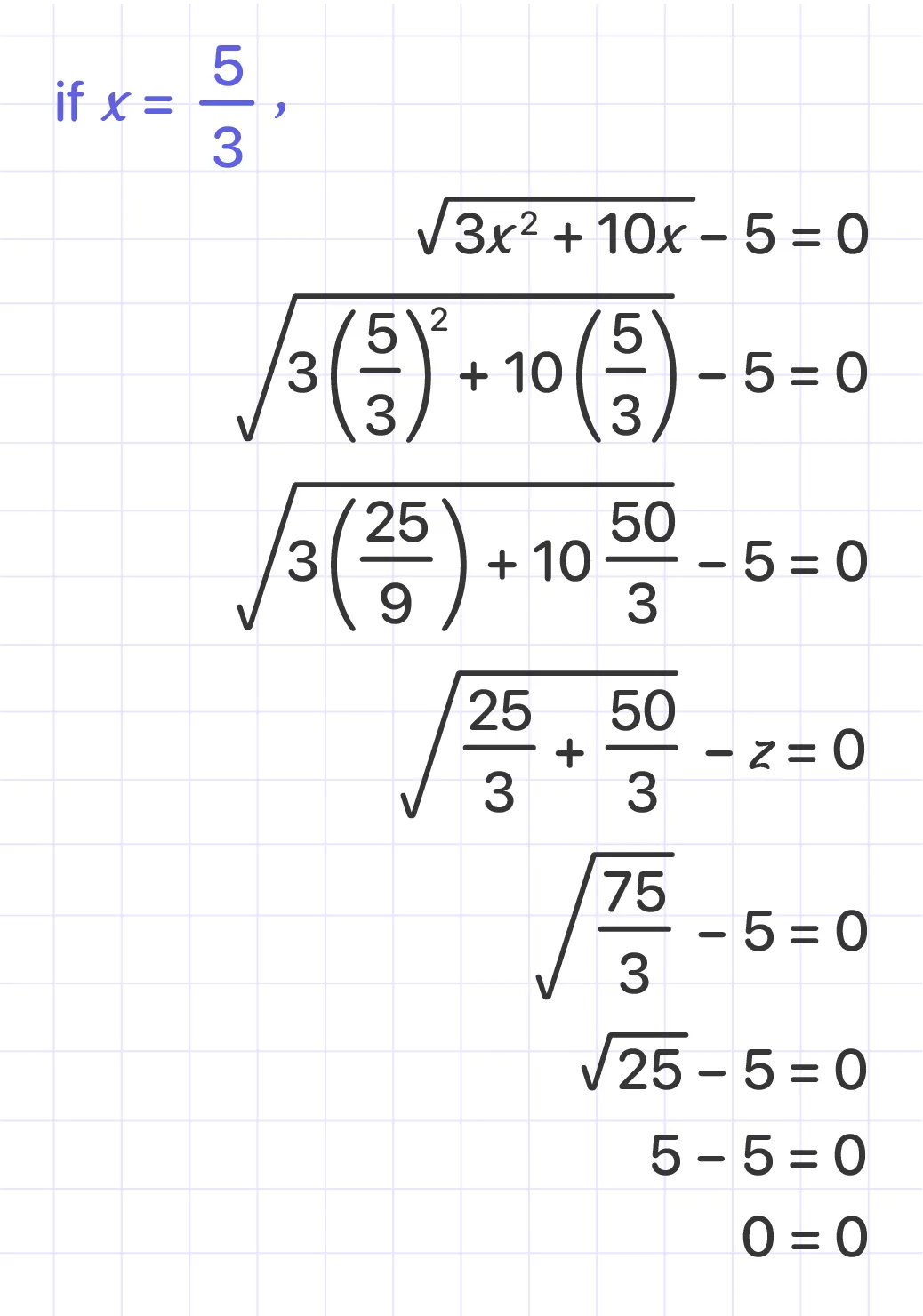
Then, we need to check the result for x = -5, so here’s what we get:

$Solution$

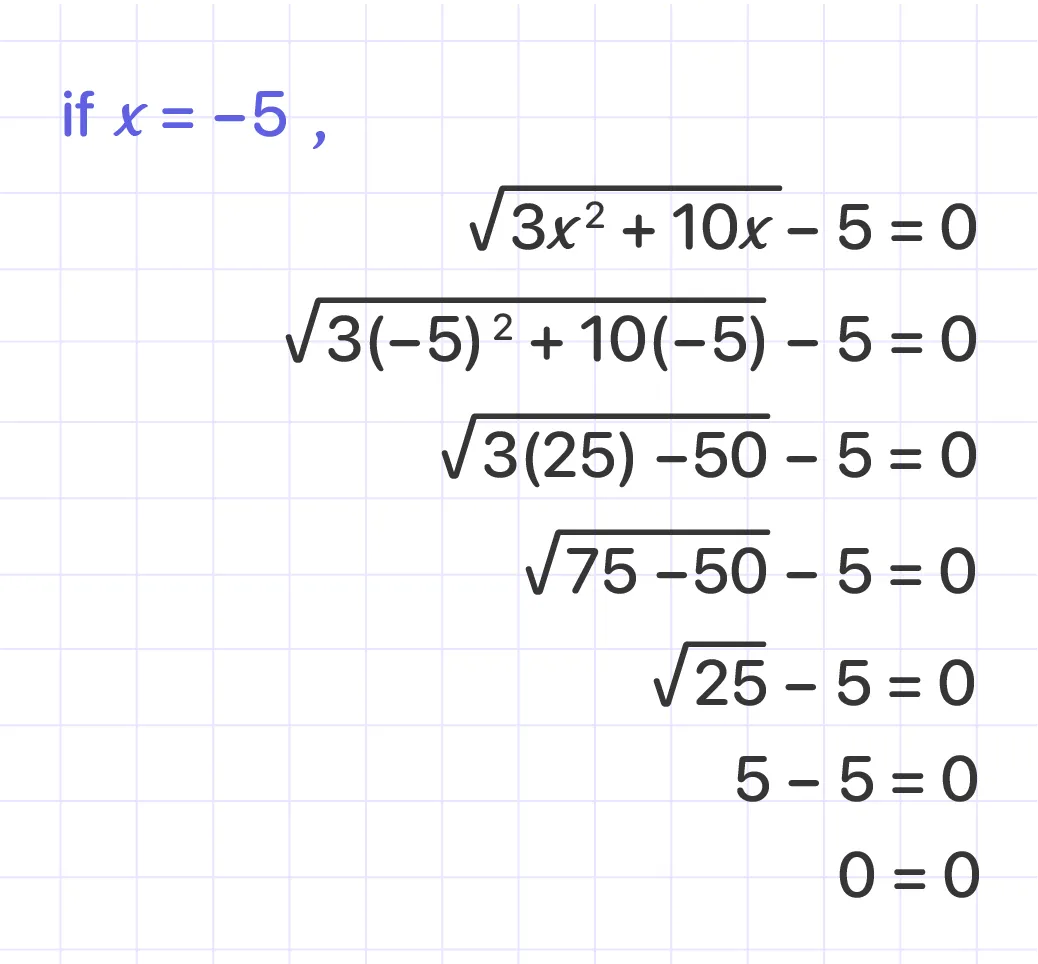
Answer: $x = -5 or x = \frac{5}{3}$.