MathMaster Blog

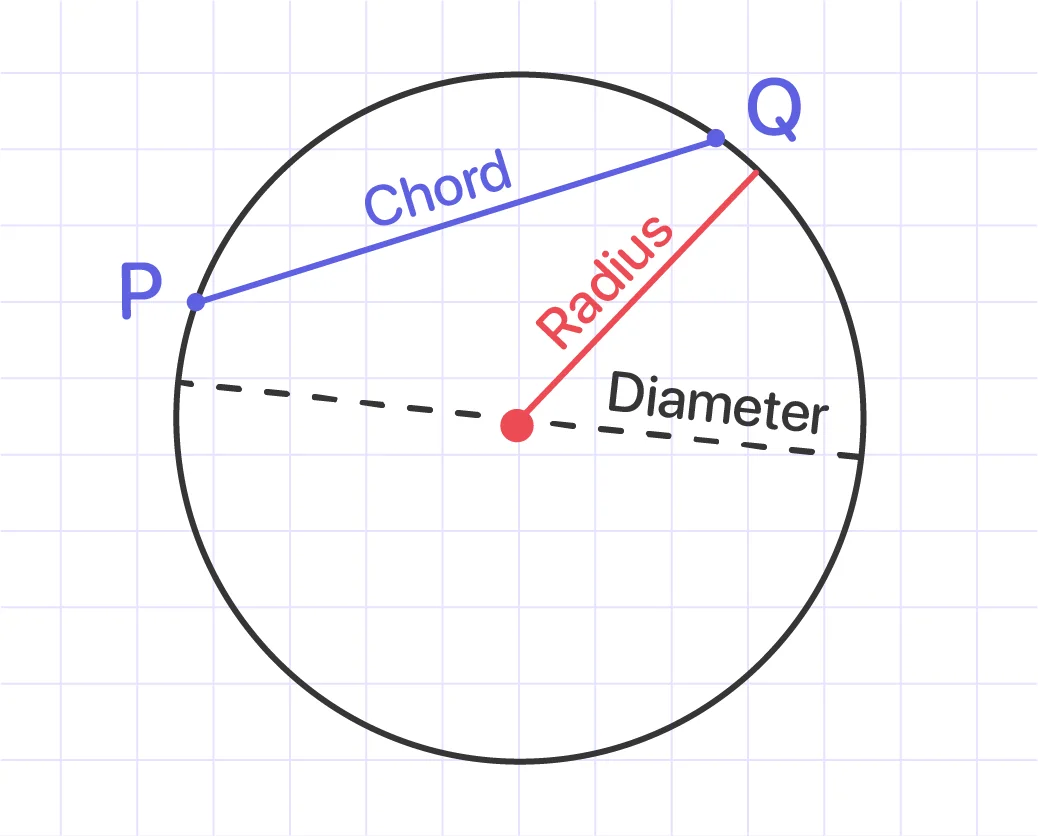
The chord of the circle is a line segment that connects two places on the circle's circumference. The diameter of a circle is considered to be the longest chord. When a circle chord is drawn, it divides the circle into two sections, which are referred to as the major and minor segments of the circle. If two chords are equidistant from the center of a circle, their lengths are equal.

There are two fundamental formulas for calculating the length of a circle's chord. Each formula is used depending on the information provided:

#1:

Based on the perpendicular distance from the center (the radius and distance to the center of a circle are known):

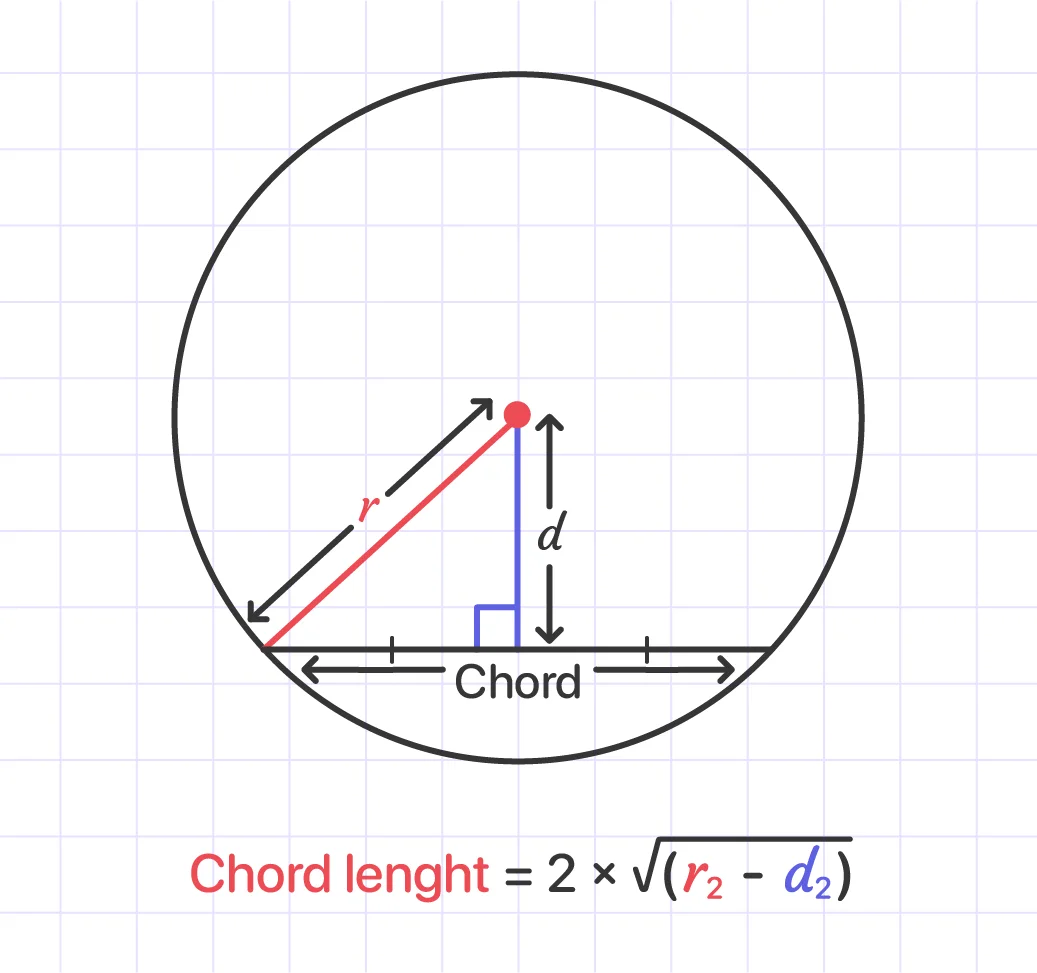#2:

Trigonometric formula (the radius and central angle are given):

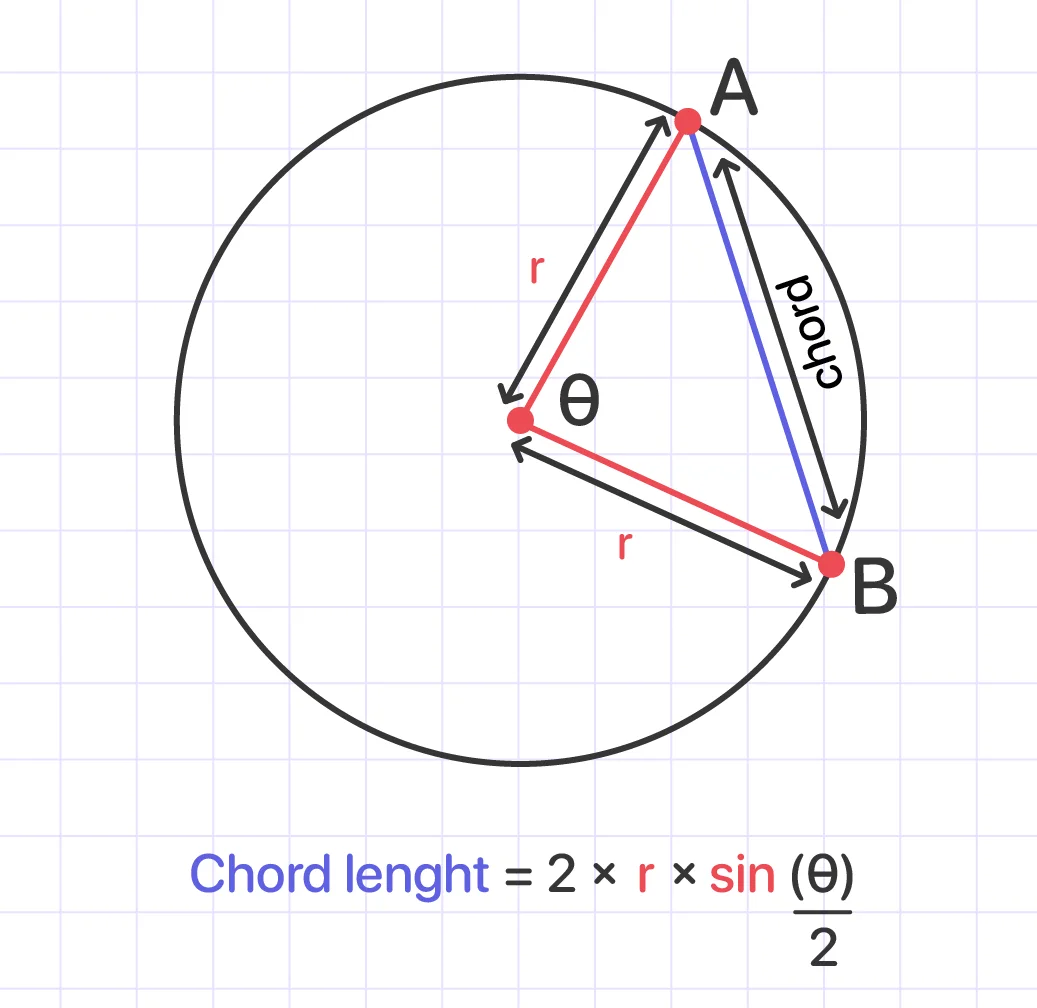
where r is the radius of the circle and θ is the angle subtended at the center by the chord.

3 basic theorems of the chord:

• The perpendicular to a chord, taken from the circle's center, bisects the chord.
• The chords of a circle that are equidistant from the circle's center are equal.
• Unequal Chords Theorem: the larger of two unequal chords in a circle will be closer to the center than the smaller chord.

Example 1:

The length of a circle's chord is 40 inches. Assume that the perpendicular distance between the center and the chord is 15 inches. What is the chord's radius?

Solution:

By the formula, 2$\sqrt{r^2 - d^2}$

2$\sqrt{r^2 - 15^2}$ = 40

2$\sqrt{r^2 - 225}$ = 40

Now, we need to square both sides.

1600 = 4(r^2- 225)

1600 = 4r^2 - 900

Add 900 on both sides.

2500 = 4r^2

Divide both sides by 4.

625 = r^2

r = -25 or 25

Because length can never be negative, we only choose positive numbers.

Answer: The radius of the circle is 25 inches.

Example 2:

Determine the length of the chord PQ in the circle below.

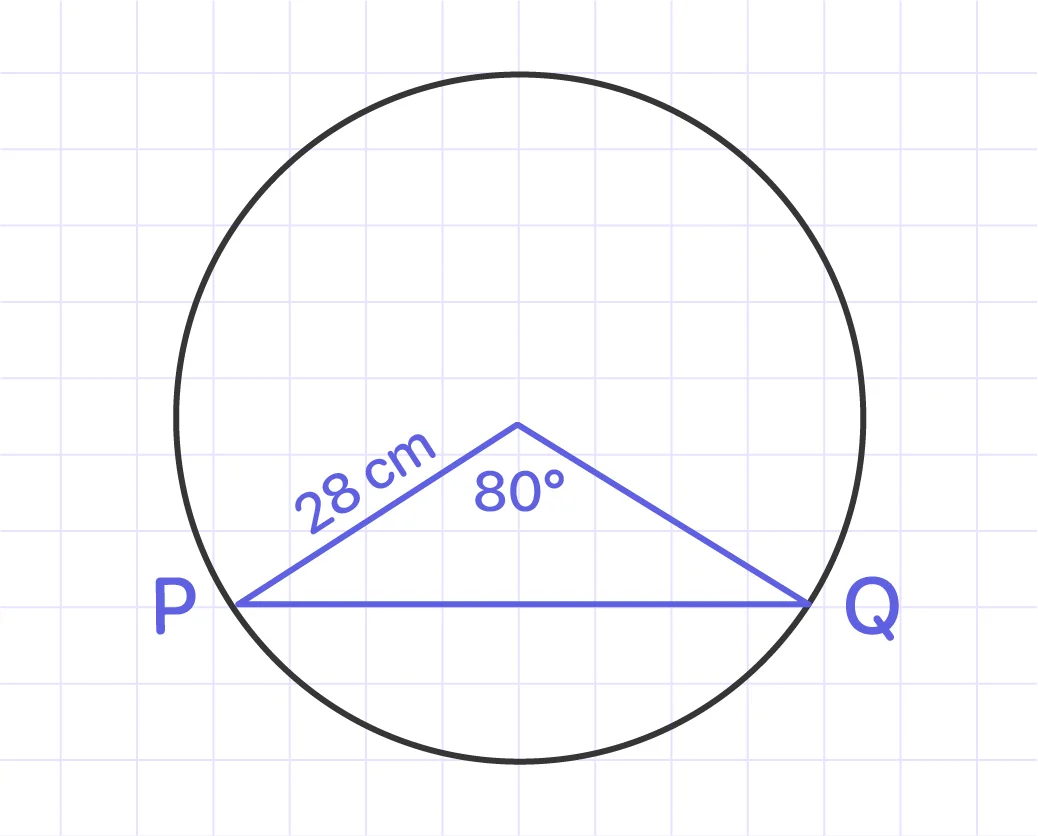
Solution:

By the formula, length of chord = 2r sine (C/2)

Substitute. Length of chord = 2r sine (C/2)

= 2 x 28 x Sine (80/2)

= 56 x sine 40

= 56 x 0.6428

= 36

Answer: The length of a chord is 36.

Example 3:

O is the center with a radius of 5 inches. Find the length of the chord AB if the length of the perpendicular drawn from the center is 4 inches.

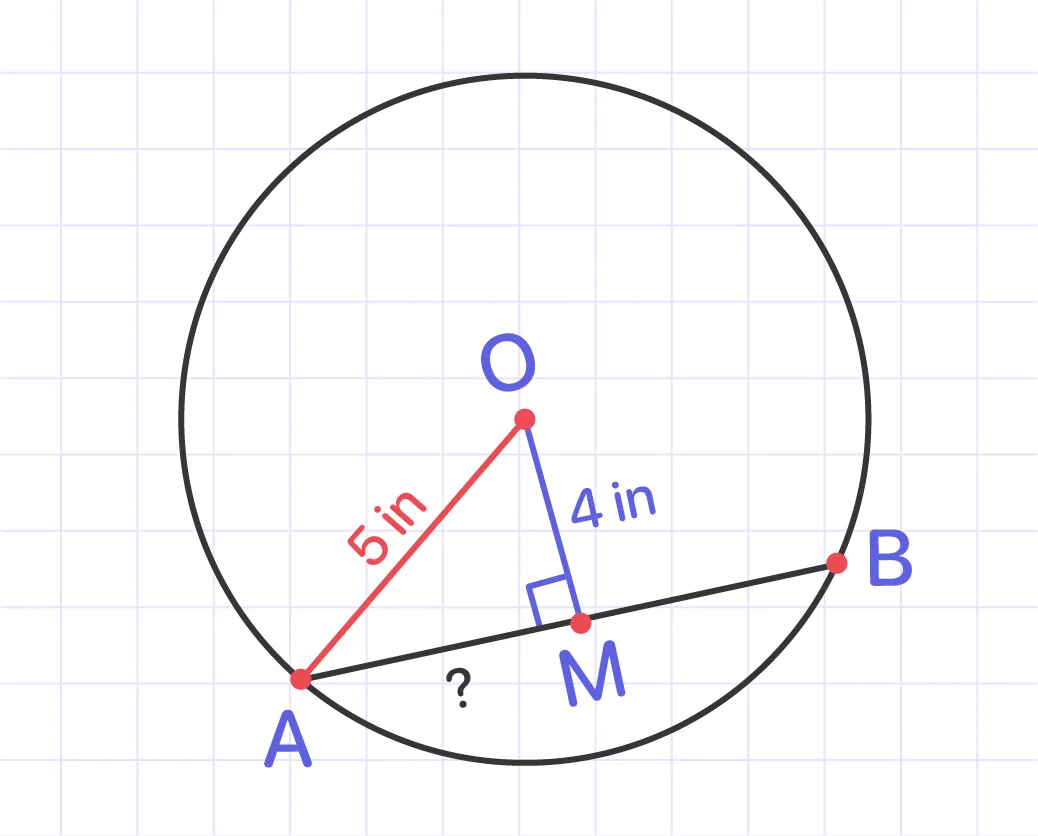
Solution:

AB is the chord of the circle. △AOM is a right-angled triangle as OM is perpendicular to AB. According to the Pythagoras theorem, OA^2 = OM^2 + AM^2.

So, after the transposition of terms, we get AM^2 = OA^2 - OM^2.

Then, we need to substitute the values:

AM^2 = 5^2 - 4^2 = 25 - 16 = 9

Thus, AM = 3.

Since OM is the perpendicular bisector of AB, so AM = MB.

Answer: Chord AB = 2 × 3 = 6 inches