MathMaster Blog

If the pairs of corresponding sides and angles of two triangles are equal, they are congruent. Here are three congruence theorems to consider:

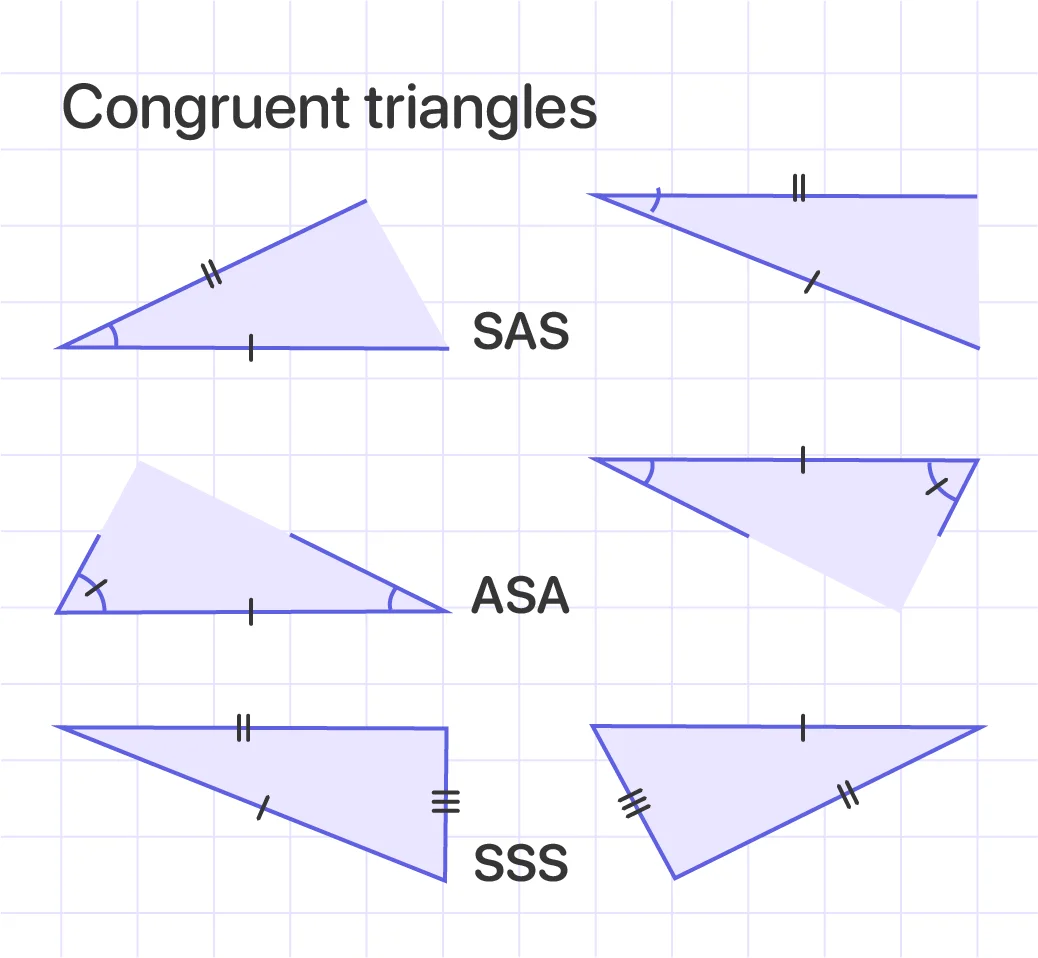
The SAS (side-angle-side) theorem: the triangles are congruent if two sides and the included angle of one triangle are equivalent to two sides and the included angle of another triangle.

The ASA (angle-side-angle) theorem: if any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle, the two triangles are congruent.

The SSS (side-side-side) theorem: if three sides of one triangle are equal to the corresponding sides of the other triangle, the two triangles are congruent.

Example 1:

RQP is an isosceles triangle. The midpoints of the triangle's equal sides are L and M. N is the third side's midpoint. Prove that LN=MN.

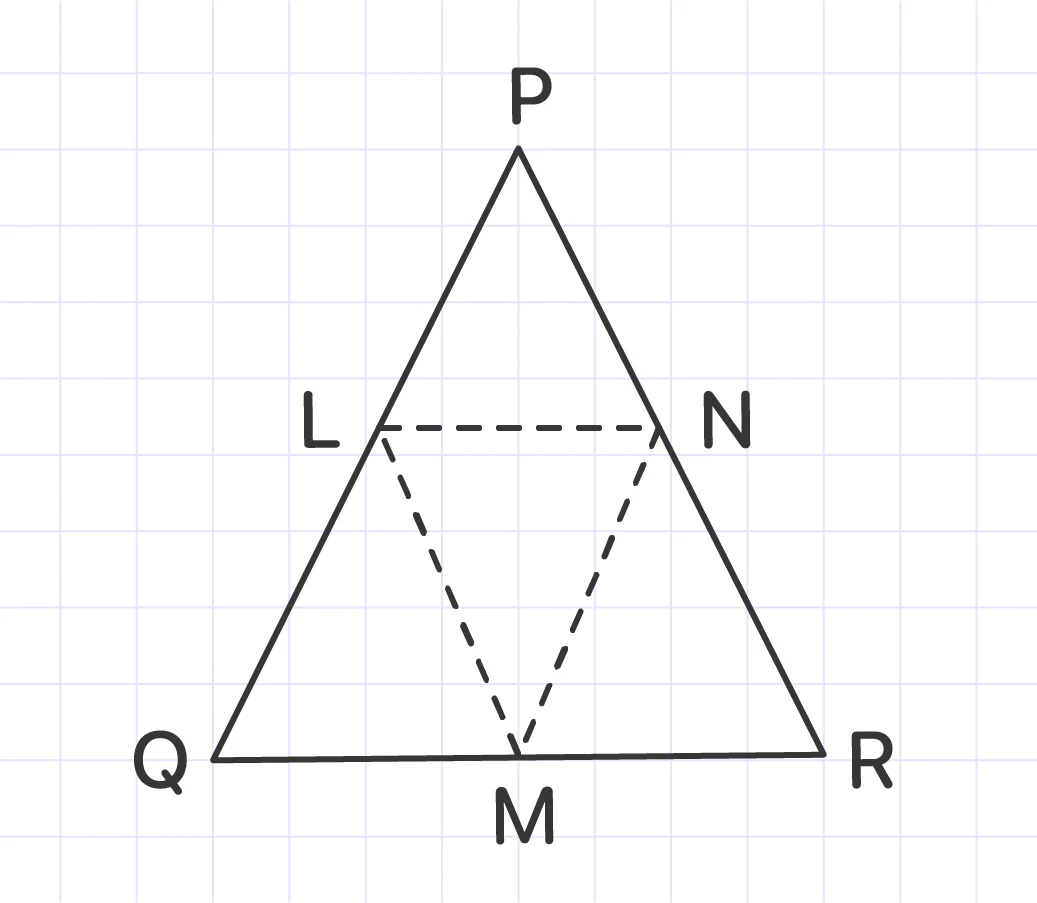
To prove that LN is equivalent to MN, all you have to do is show that ΔLPN ≅ ΔMRN.

PQ = QR (In an isosceles triangle, the two sides are equal)

∠QPR = ∠PRQ (Angles that are opposite to equal sides are also equal)

PL = LQ = QM = MR

For ΔLPN and ΔMRN:

LP = MR (Because L and M are midpoints and PQ = QR)

∠LPN = ∠MRN (Because ∠QPR = ∠QRP)

PN = NR (Since N is the midpoint of PR)

Then, using the SAS congruence in triangles criterion, we can state that ΔLPN ≅ ΔMRN.

Answer: Given the fact that the corresponding sections of congruent triangles are equal, LN=MN.

Example 2:

Determine the congruence statement.

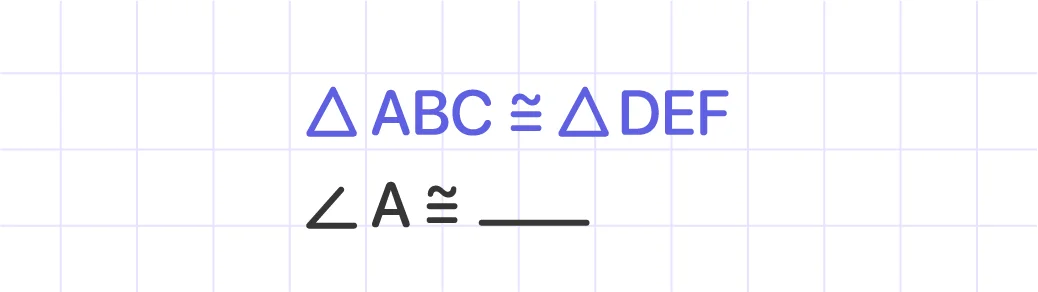
Solution:

Because the triangles are congruent, their angles and sides must also be congruent. ∠A and ∠D are corresponding angles, so ∠A ≌ ∠D.

Answer: ∠A ≌ ∠D