Derivatives

A derivative of a function is the rate of change of one quantity over the other. The derivative tells us the slope of a function at any point. The derivative of f(x) with respect to x is the function f ′( x ) and is defined as

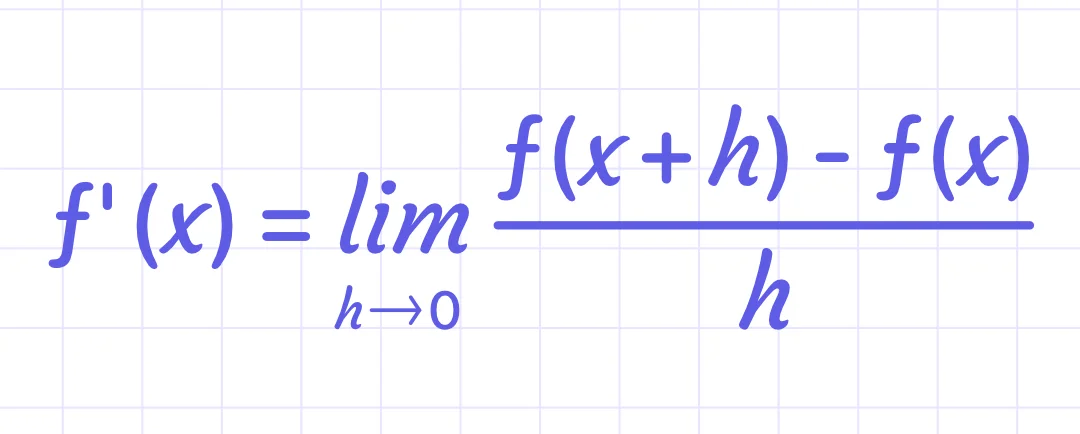
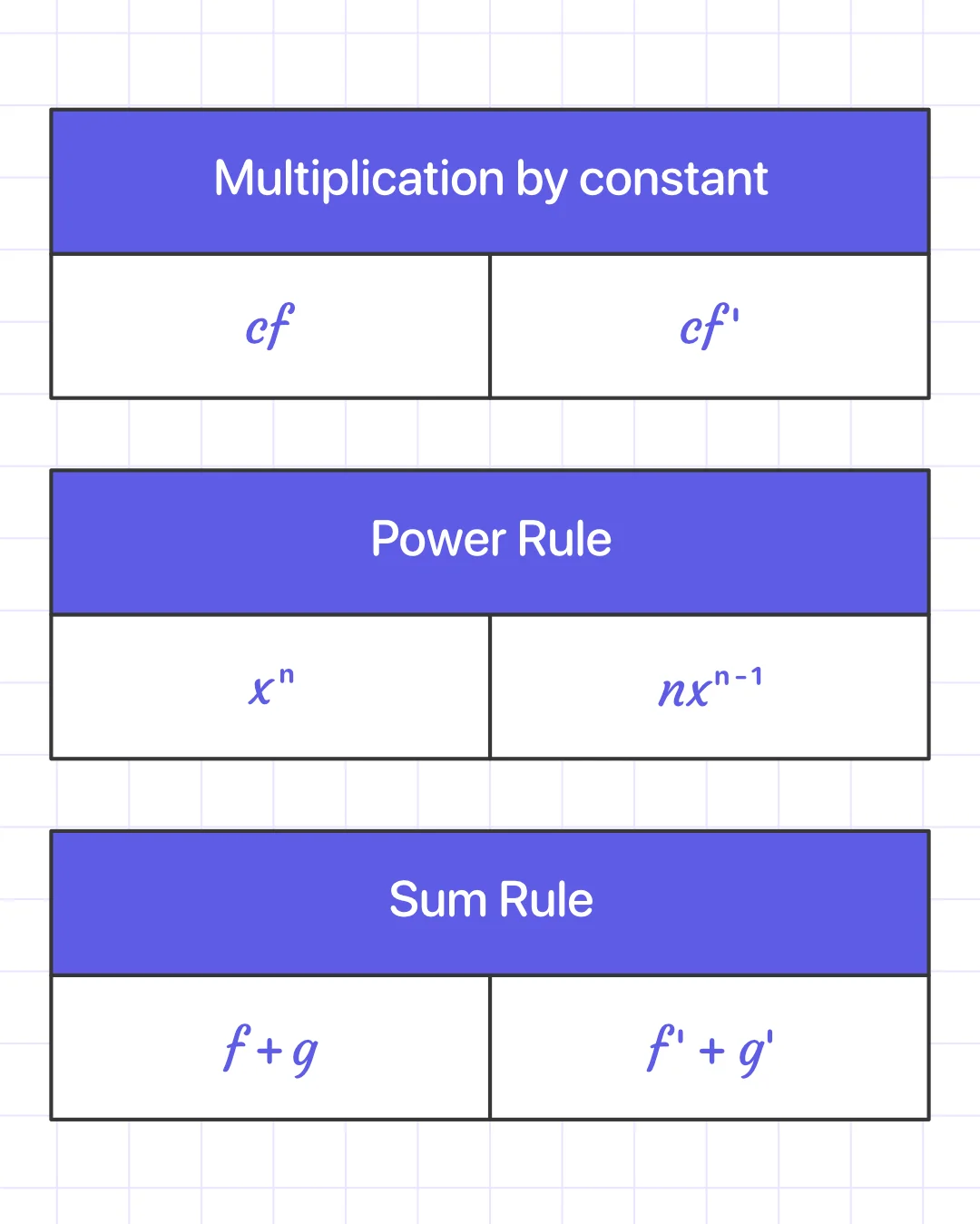
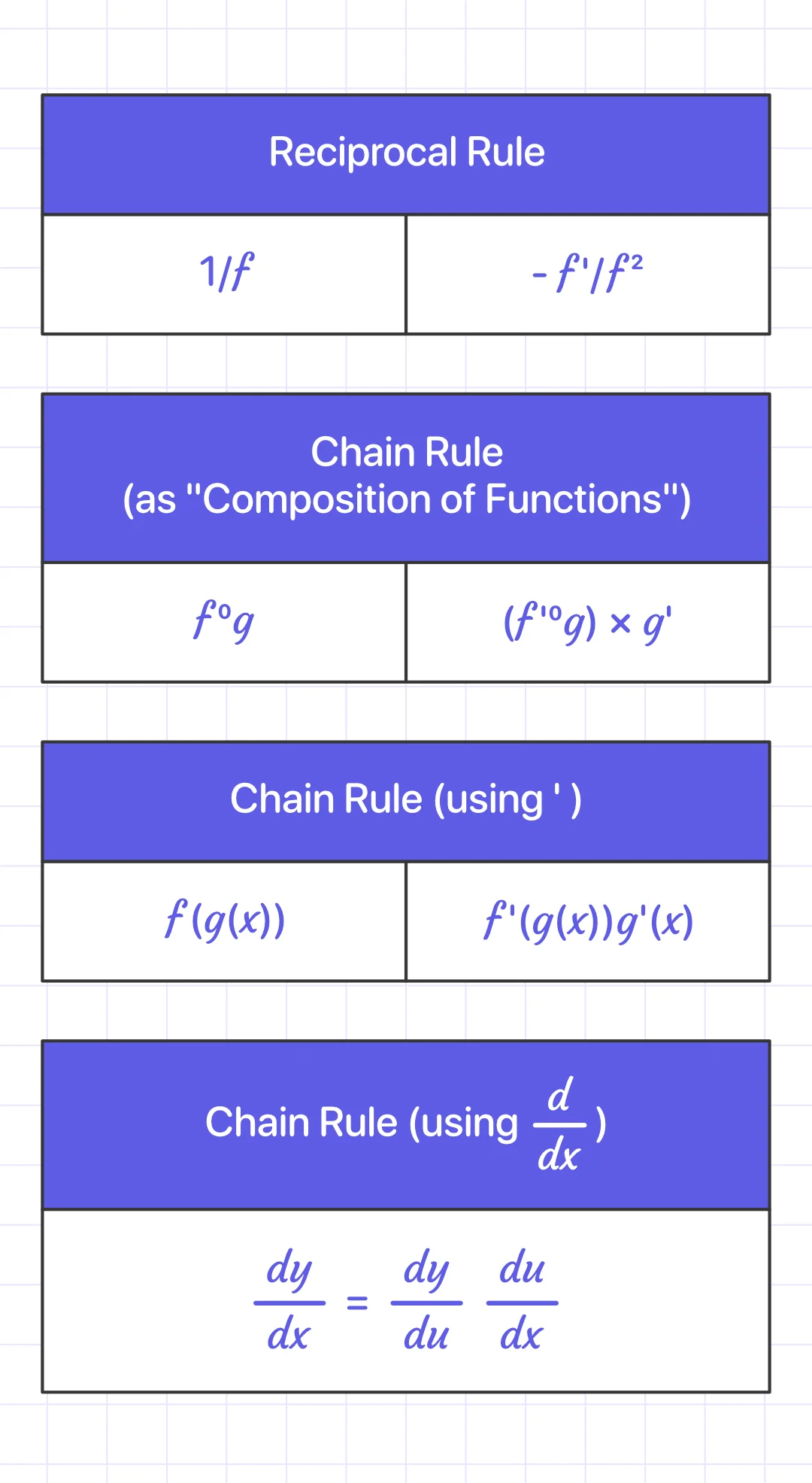
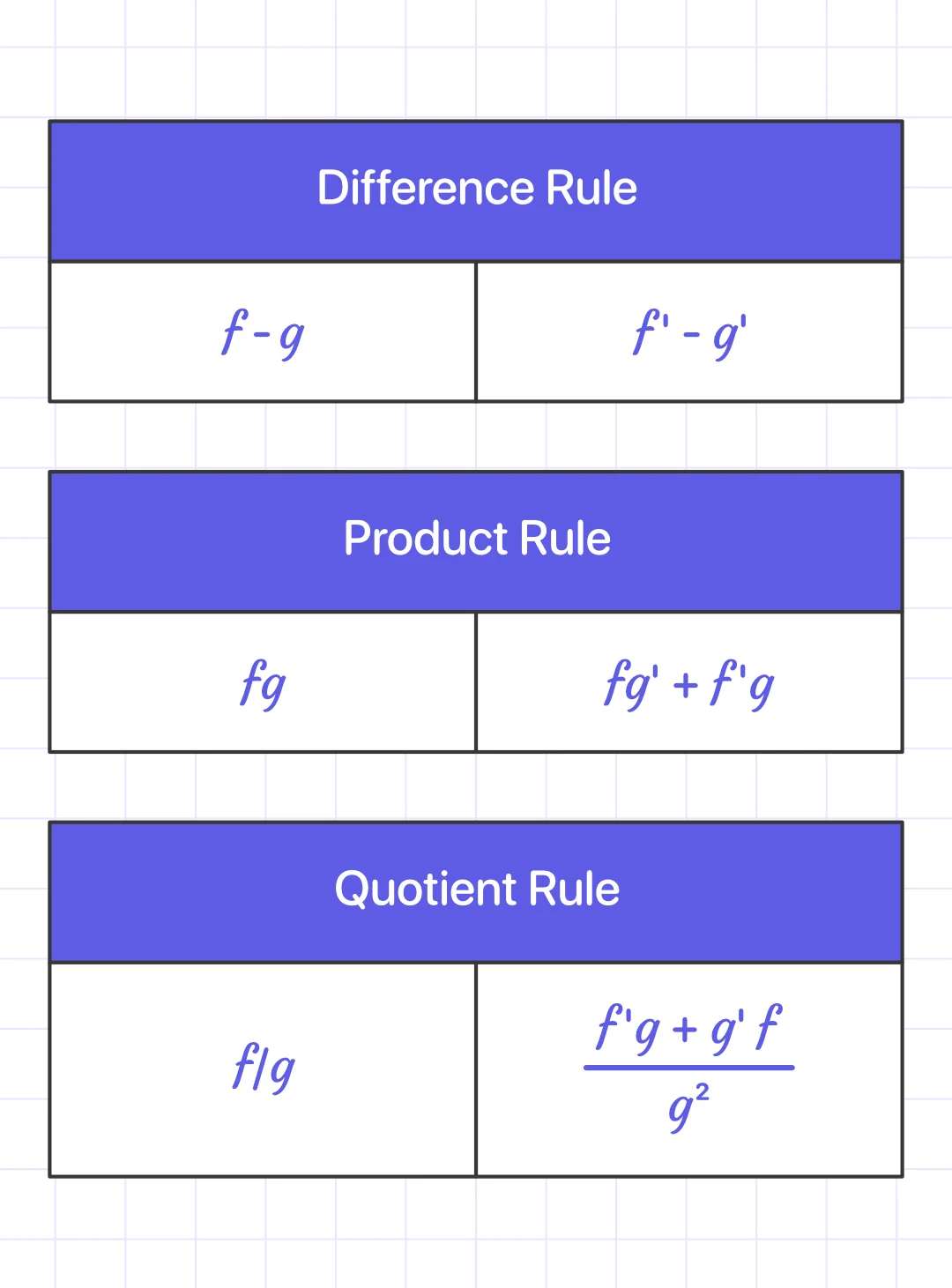
Set of rules to find derivatives:

Example 1:

$y = (2x + 3)^{3x - 5}$

Use logarithmic differentiation to find the derivative dy/dx.

Solution:

Example 2:

Find the derivative of the curve y = [(x + 3)(x+2)]/x^2 at the point (3,0).

Solution:

y = (x^2 + 5x + 6)/x^2 = 1+ 5/x + 6/x^2

The derivative of the curve is dy/dx = d/dx. 1+ d/dx . 5/x + d/dx.

6/x^2

dy/dx = d/dx. 1 + 5.d/dx^(-1) + 6.d/dx.x^(-2)

= 0 + 5(-1.x^(-2)) + 6. (-2.x^(-3))

(applying the Power Rule of derivatives)

= -5/x^(-2) - 12x^(-3)

The derivative of the curve at x = 3 is dy/dx = -5/3^2 - 12/3^3

= -5/9 - 12/27

=-27/27

= -1

Answer: The derivative of the curve y = [(x + 3)(x+2)]/x^2 at the point (3,0) is -1.

Example 3:

f`(x) = $\lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$

Prove from first principles that the derivative of x^2 is 2x.

Solution:

Let’s suppose that f(x) = x^2. So, by the first principle,

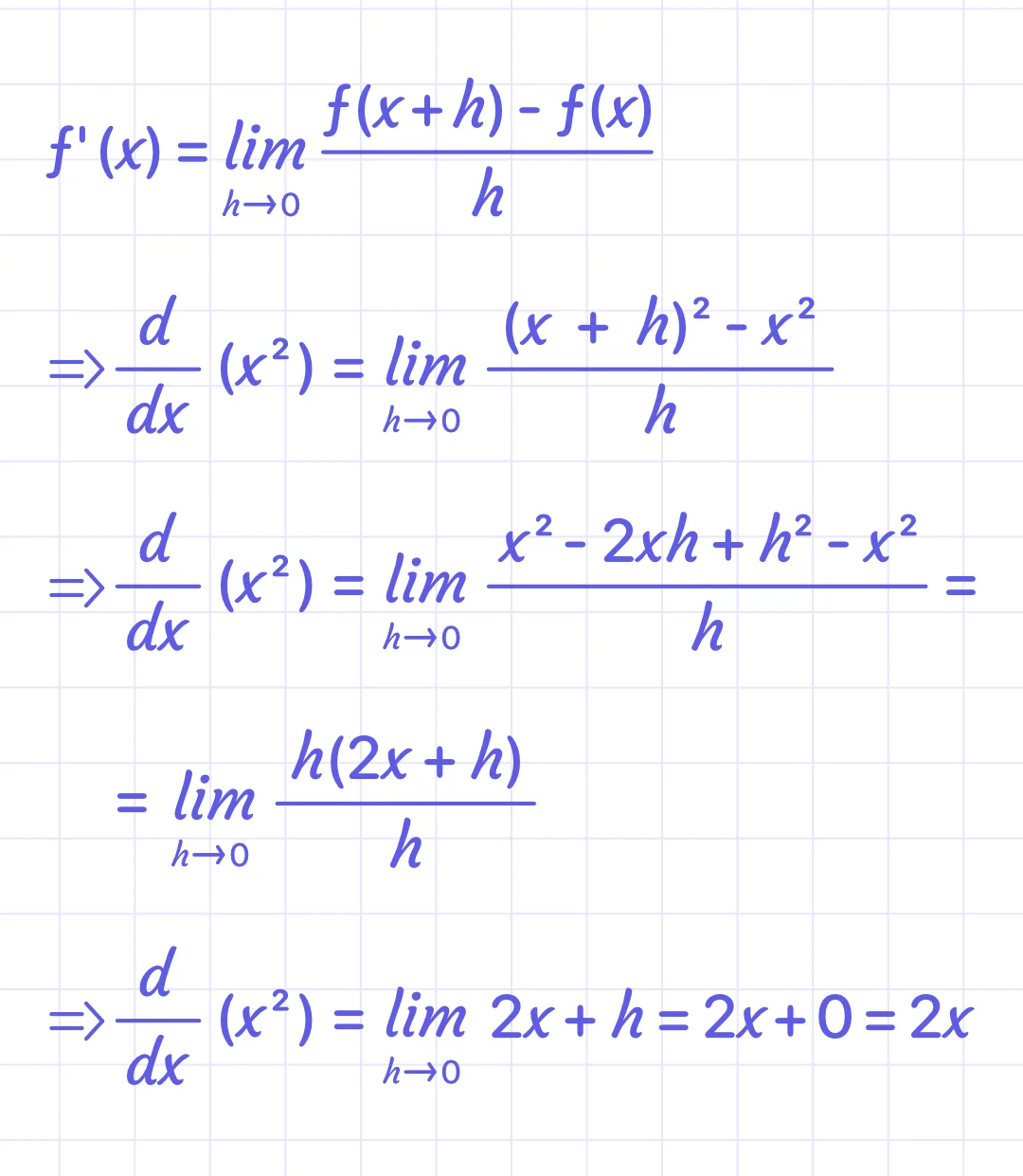
Answer: The derivative of x2 is 2x. Thus, the statement is proved.