MathMaster Blog

Find the tangent using the formula:

tan(θ) = Opposite / Adjacent

Example 1:

Find the tangent of the angle:

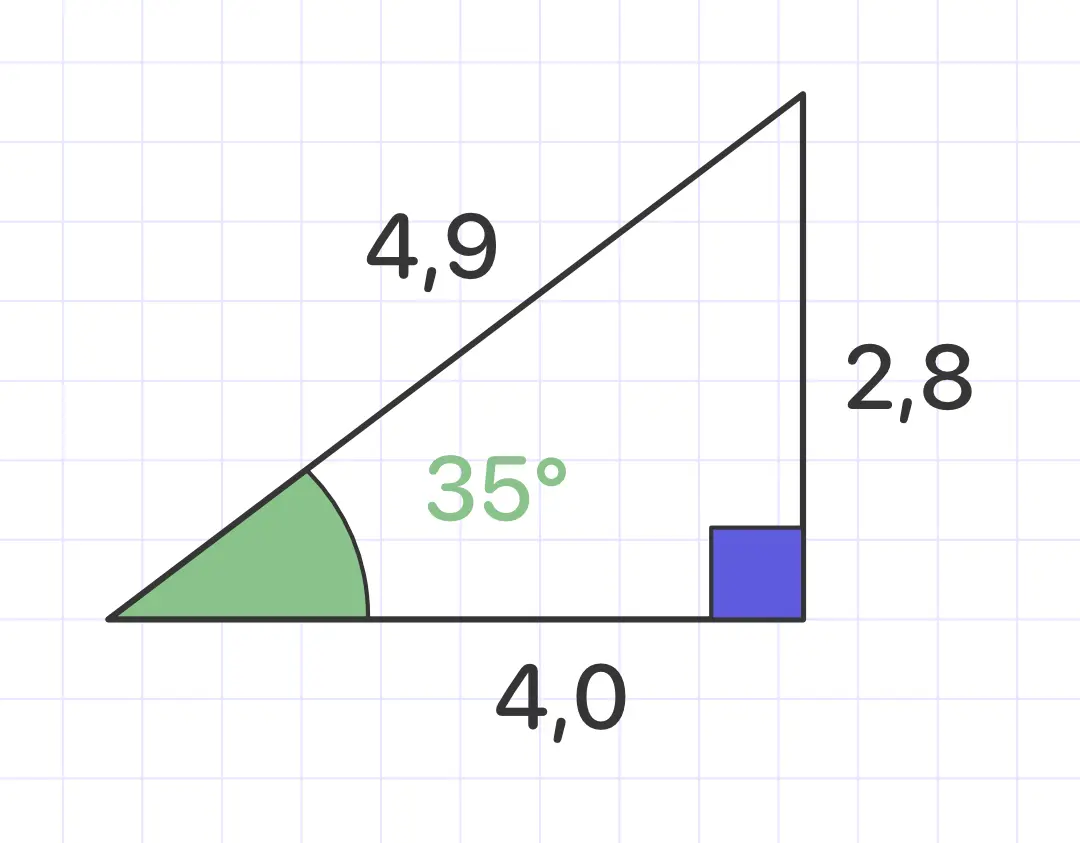
Solution:

Example 2:

Find the exact of $tan^{-1}(-\sqrt{3})$

Solution:

Let $θ = tan^{-1}(-\sqrt{3})$. We seek the angle θ, -π/2 < θ < π/2, whose tangent equals -√3.

θ = $tan^{-1}(-\sqrt{3})$ - π/2 < θ < π/2

tan(θ) = -√3 - π/2 < θ < π/2

The only angle θ within the interval -π/2,π/2 whose tangent is -√3 is -π/2.

Answer $tan^{-1}(-\sqrt{3}) = π/3$