MathMaster Blog
A parallelogram is a four-sided, two-dimensional figure with the following properties:
- two equal and opposing sides
- two intersecting but non-equal diagonals, and
- two equal and opposite angles
A parallelogram's area is calculated by multiplying its base by its altitude. The base and altitude of a parallelogram are perpendicular to each other.
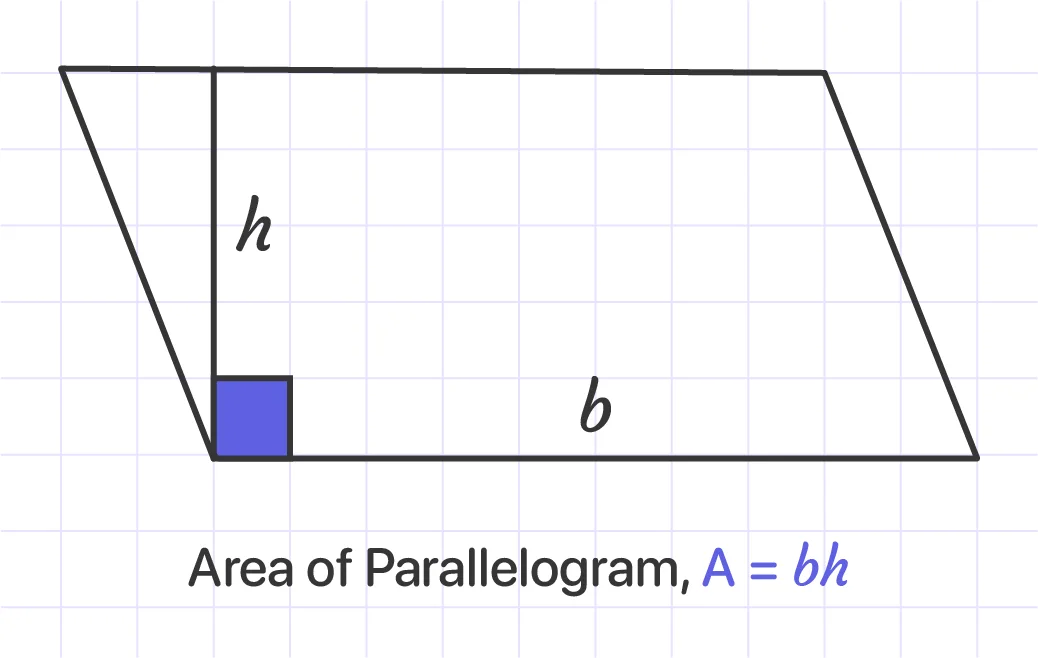 #2:
#2:
If the length of neighboring sides and the angle between them are known, the area of a parallelogram can be determined without the height. In this case, we can use the area of the triangle formula from the trigonometry concept:
Area = ab sin (θ)
Where:
a and b = length of parallel sides, and,
θ = angle between the sides of the parallelogram
#3:The length of a parallelogram's diagonals can also be used to calculate its area.
Area = ½ x d1x d2sin(x)
Where:
d1 and d2 = length of the diagonals, and,
x = angle between the diagonals
Example 1:
Calculate the area of a parallelogram with 18 cm and 15 cm diagonals and a 43° angle of intersection between them.
Solution:
Let d1 = 18 cm and d2 = 15 cm.
β = 43°
A = ½ x d1 x d2 sine (β)
= ½ x 18 x 15 sine (43°)
= 135 sine (43°)
= 92.07 cm2
Answer: The area of the parallelogram is 92.07 cm^2
Example 2:
Calculate the height of a parallelogram with parallel sides of 30 cm and 40 cm and a 36-degree angle between them. Assume that the parallelogram's base is 40 cm.
Solution:
Area = ab sine (a) = bh
30 x 40 sine(36) = 40 x h
1.200 sine(36) = 40 x h
Divide both sides by 40.
h = (1200/40) sine 36
= 30 sine 36
h = (1200/40) sine 36
= 30 sine 36
h = 17.63 cm
Answer: The height of the parallelogram is 17.63 cm.