MathMaster Blog

The cotangent of an angle in a right triangle is the ratio of the adjacent side (the side adjacent to the angle) to the opposite side (the side opposite to the angle).

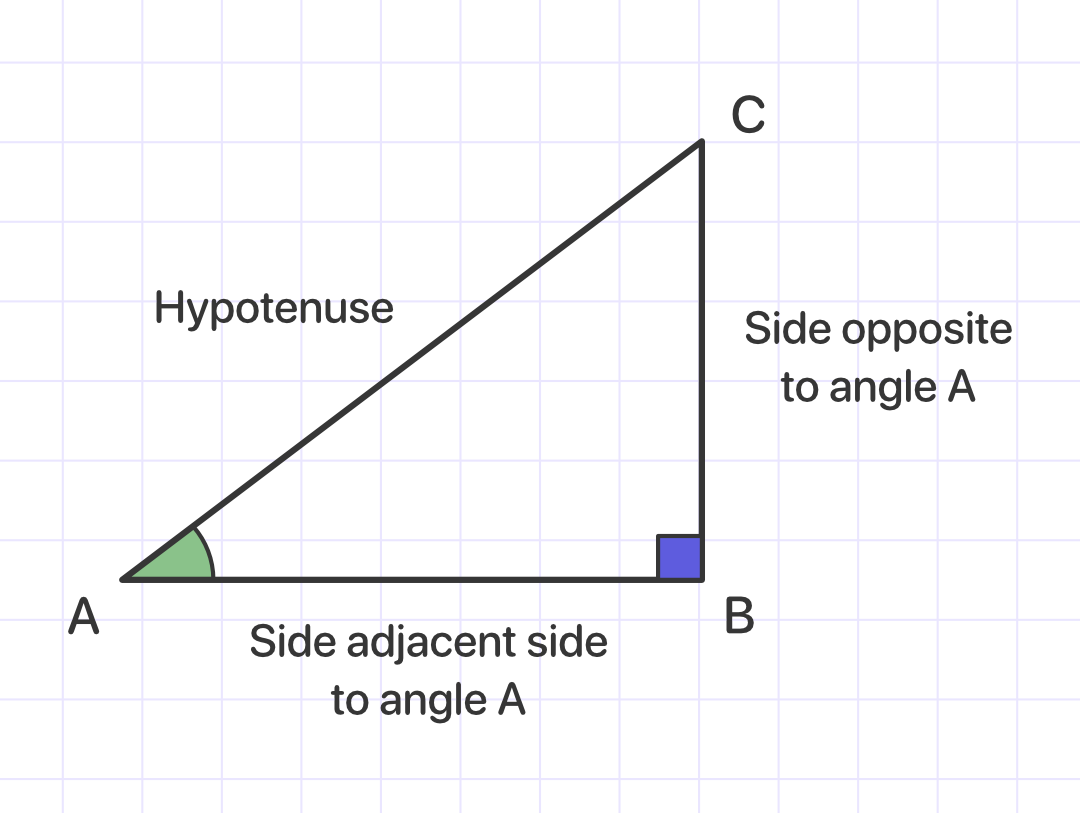
Example 1:

Evaluate cot (x - π) + cot (2π - x) + cot x.

Solution:

Apply these cotangent formulas:

cot (-x) = -cot x

cot (π-x) = -cot x

cot (2π - x) = -cot x

So, here’s what we get:

cot (x - π) + cot (2π - x) + cot x

= - cot (π-x) + cot (2π - x) + cot x

= -(-cot x) - cot x + cot x

= cot x

Answer: cot (x - π) + cot (2π - x) + cot x = cot x

Example 2:

Find the cotangent of x if sin x = 3/5 and cos x = -4/5 using the cotangent formula.

Solution:

cot x = (cos x) / (sin x)

= (-4/5) / (3/5)

= -4/3

Answer: cot x = -4/3