MathMaster Blog

A prism is a solid three-dimensional shape with two identical faces and other faces that resemble a parallelogram. The unit of volume of a prism is given as cubic meters, cubic centimeters, cubic inches, or cubic feet, etc.

The volume of a prism is calculated by multiplying the area of the base by the prism's height.

V = Bh

Example 1:

The width of a rectangular prism is doubled, its length is tripled, and its height is cut in half. If the volume of the original prism was V, what is its new volume?

Solution:

The volume of the original prism was

V = l x ω x h

The volume of the new prism is

V = 2l x 3ω x (1/2)h = 3l x ω x h = 3V

Answer: The prism volume is 3V.

Example 2:

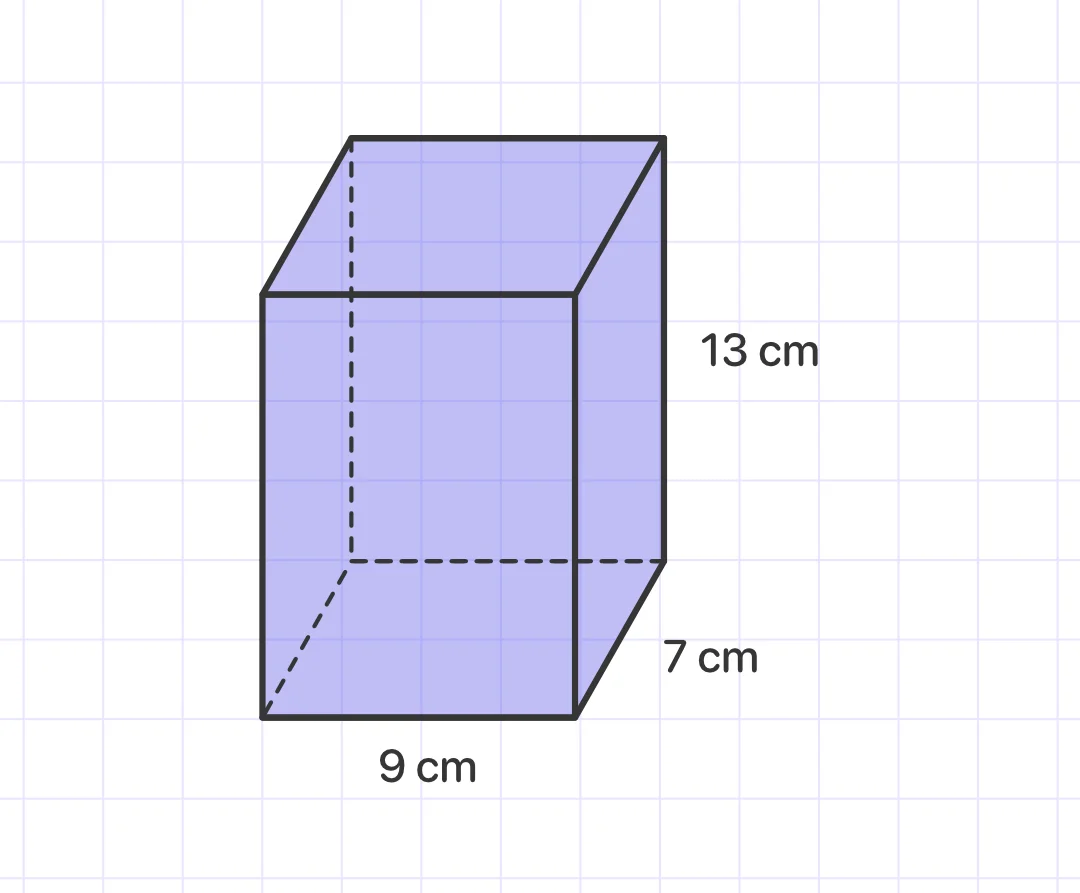
Find the volume of a prism below:

Solution:

The volume of a prism is calculated using the formula V = Bh, where B is the base area and h is the height.

The prism's base is a rectangle. The rectangle's length is 9 cm and its width is 7 cm.

A = lw is the area of a rectangle with length l and width w.

So, the base area is 9 x 7 or 63 cm^2.

As the height of the prism is 13 cm, we need to substitute 63 for B and 13 for h in V = Bh.

V = (63)(13)

Now, we need to multiply: V = 819

Answer: The volume of a prism is 819 cubic centimeters.

Example 3:

Calculate the prism's height if its volume is 729 cubic units and its base area is 27 square units.

Solution:

Let the height of the prism be "H".

To calculate it, we need to substitute the values in the volume of the prism formula:

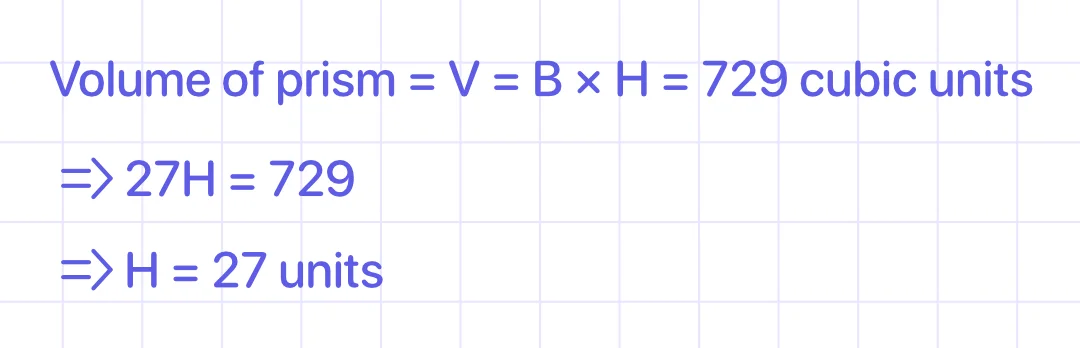
Answer: The height of the prism is 27 units.