MathMaster Blog

Logs (or) logarithms are another way of expressing exponents.

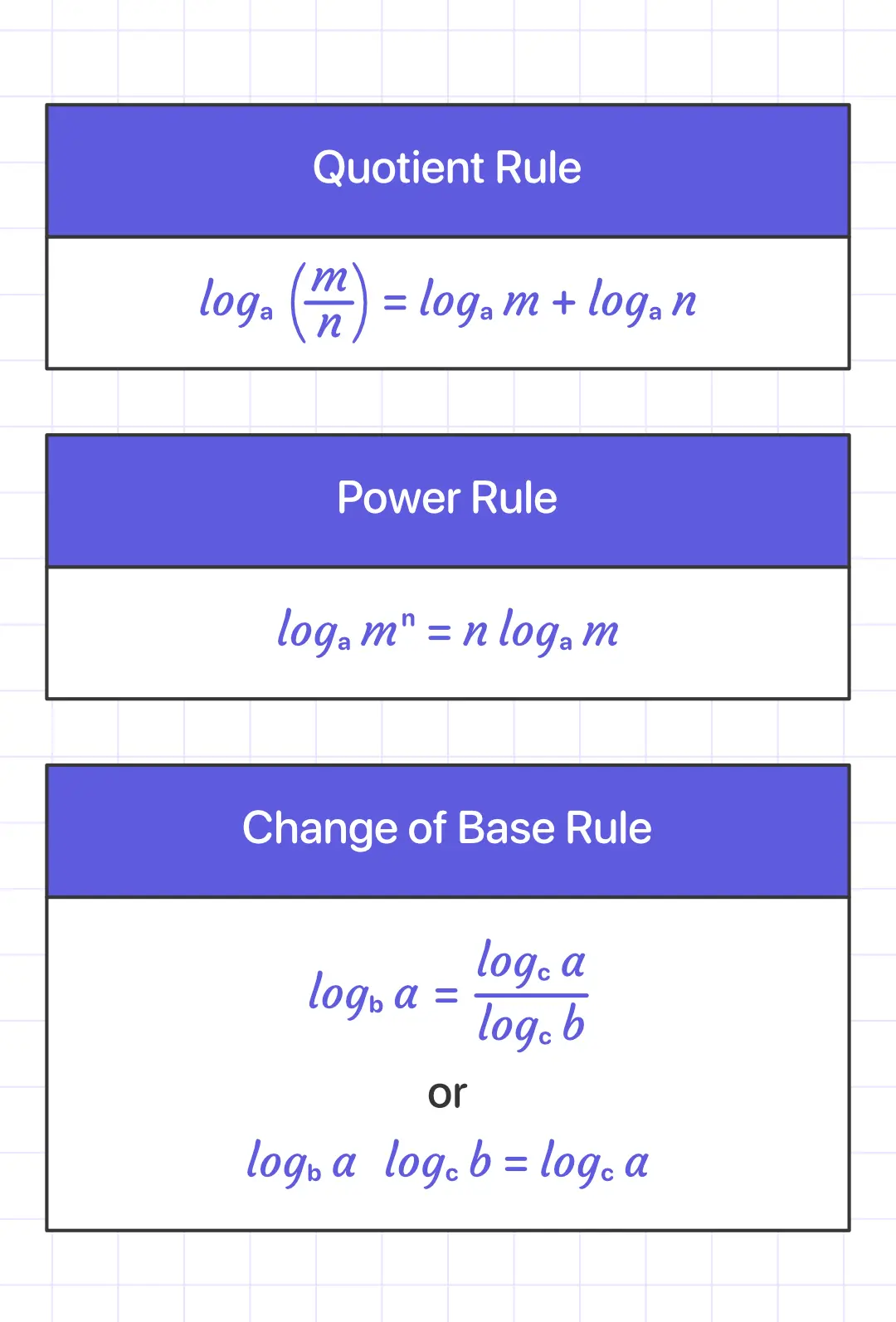
Essential rules of logarithms you should remember & use:

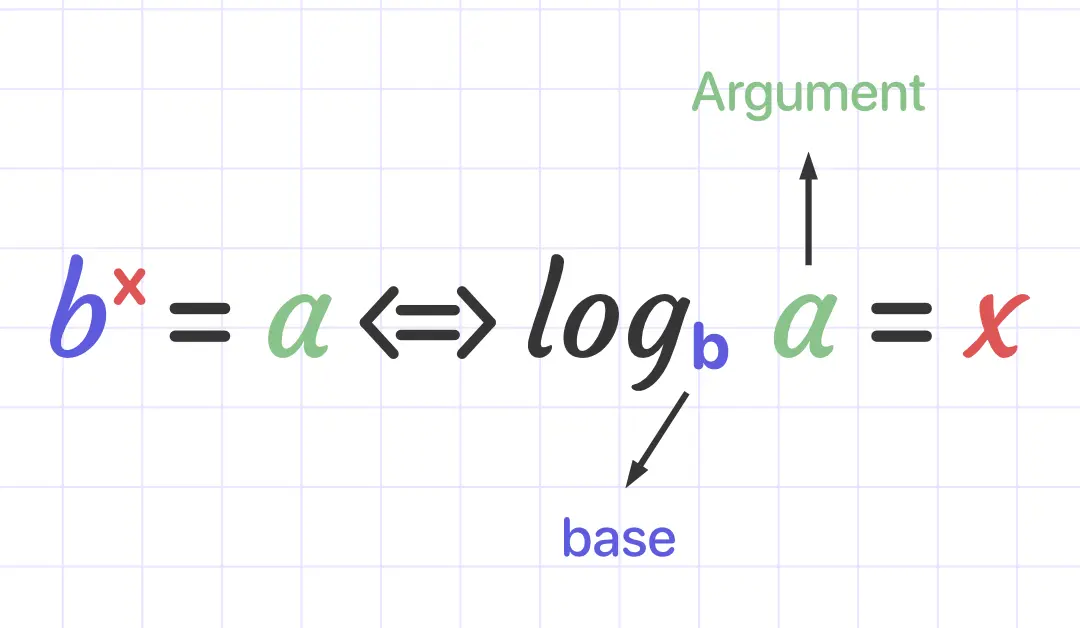
The structure of a logarithm:

Example 1:

Convert to logarithmic form $12^{x/6}$ = 18

Solution:

Convert the exponential equation to a logarithmic equation using the logarithm base (12) of the right side (18) equals the exponent (x/6).

Answer: $log_{12}18$ = x/6

Example 2:

Express 4^3 = 64 in logarithmic form.

Solution:

The exponential form a^x = N can be written in logarithmic function form as

$log_{a}N$ = x

So, 4^3 = 64 can be written as $log_{4}64$ = 3

Answer: $log_{4}64$ = 3

Example 3:

Simplify $log_{2}(1/128)$

Solution:

To simplify the provided logarithm, we apply the properties of logarithmic functions.

$log_{2}(1/128)$ = $log_{2}1$ - $log_{2}128$

= 0 - $log_{2}2^{7}$

= -$log_{2}2^{7}$

= $-7log_{2}2$

= -7(1)

= -7

Answer: $log_{2}(1/128)$ = -7