MathMaster Blog

A system of equations is a set of 2 or more equations with the same variables.

A solution to a system of equations is a set of values that makes each equation in the system true.

Graphing

One of the methods for solving a system of linear equations is graphing.

Example:

Solve the system of linear equations

• y = 3x + 7
• y = –4x

Solution:

Step1:

Graph the first equation y = 3x + 7.

You can do it by plotting the y-intercept, 7, and then using the slope, 3, because y = 3x + 7 is a slope-intercept form (y = mx + b).

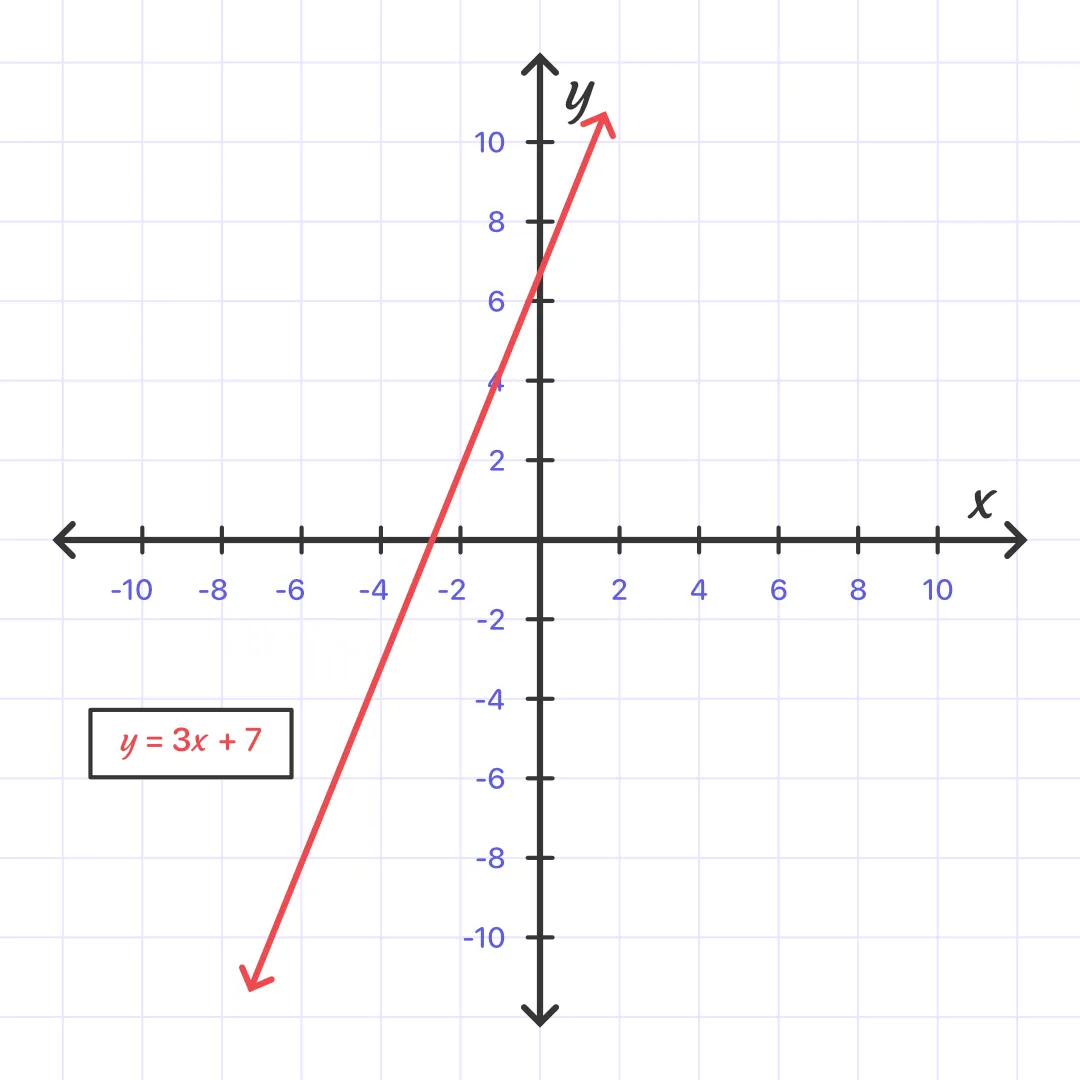
Step2:

Graph y = –4x by plotting the y-intercept, 0, and then using the slope, – 4.

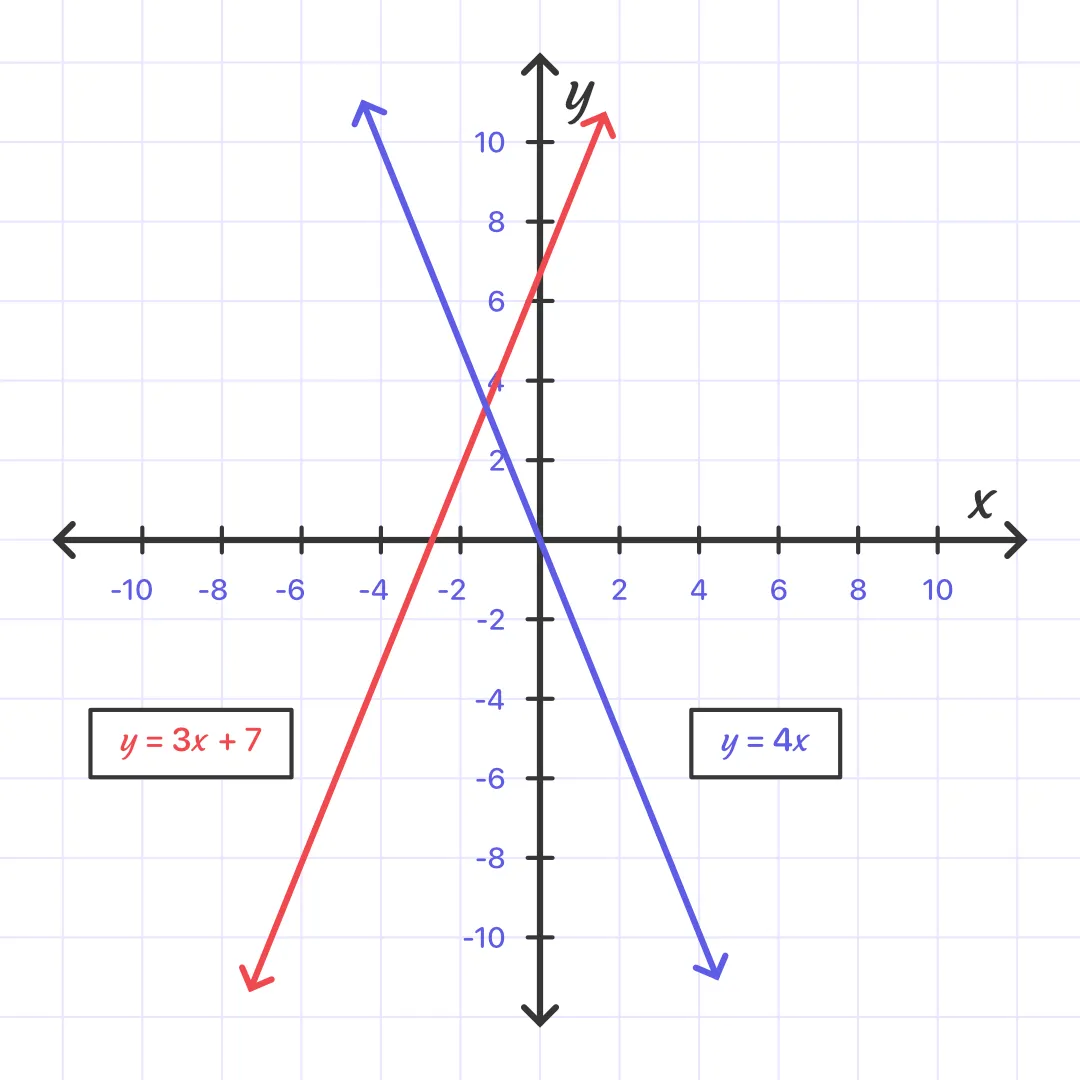
Step3:

Find the point where the lines intersect.

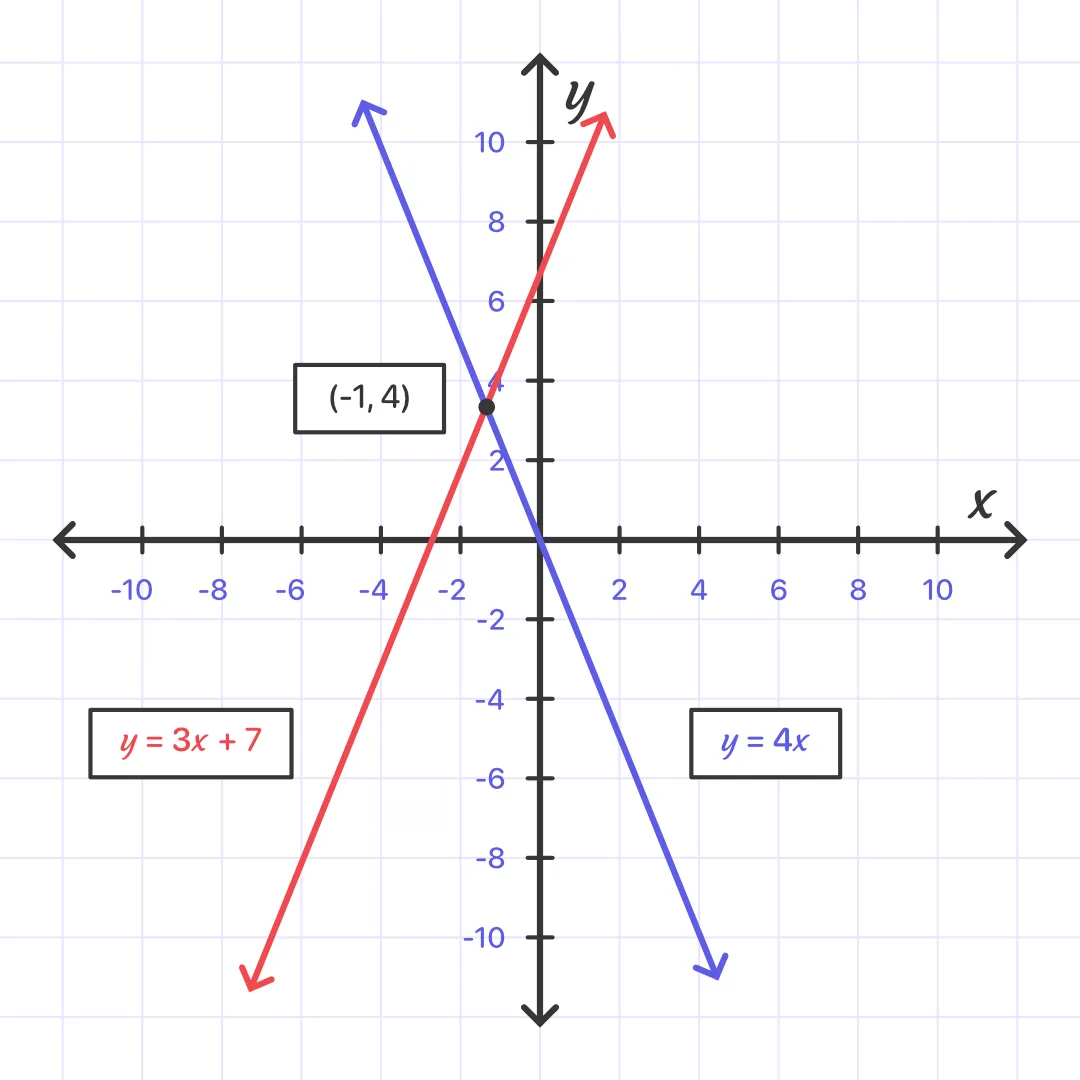
Answer: Therefore, the solution to this system of equations is ( – 1, 4).

Tip:

To check whether the solution is correct, substitute values in the system of equations (-1 for x and 4 for y):

y = 3x + 7

4 = 3(-1) + 7

4 = -3+7

4 = 4

y = –4x

4 = –4(-1)

4 = 4