MathMaster Blog

An exponential function has the form of f(x) = a^x, where x is a variable and a is a constant which is called the base of the function. A should be greater than 0.

• Properties of the exponential function depend on the value of a.
• A never crosses the x-axis.
• When a = 1, the graph is presented by a horizontal line at y = 1.

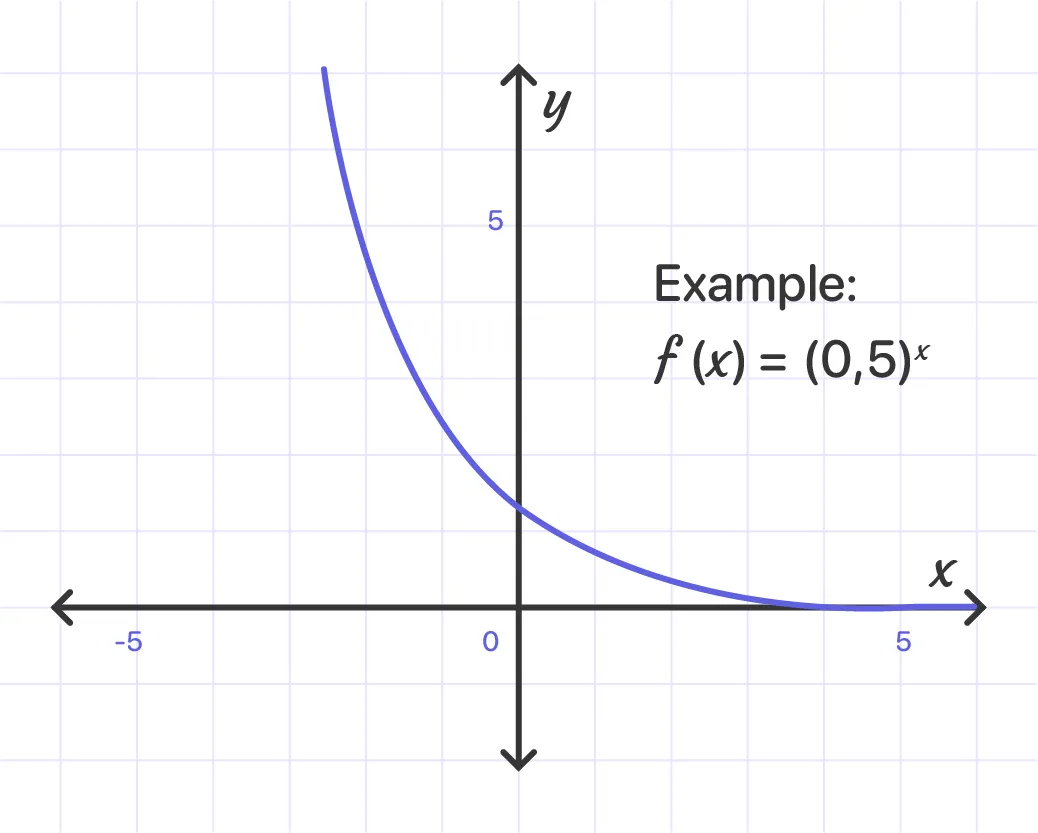
• When a is between 0 and 1, we graph it this way:

  

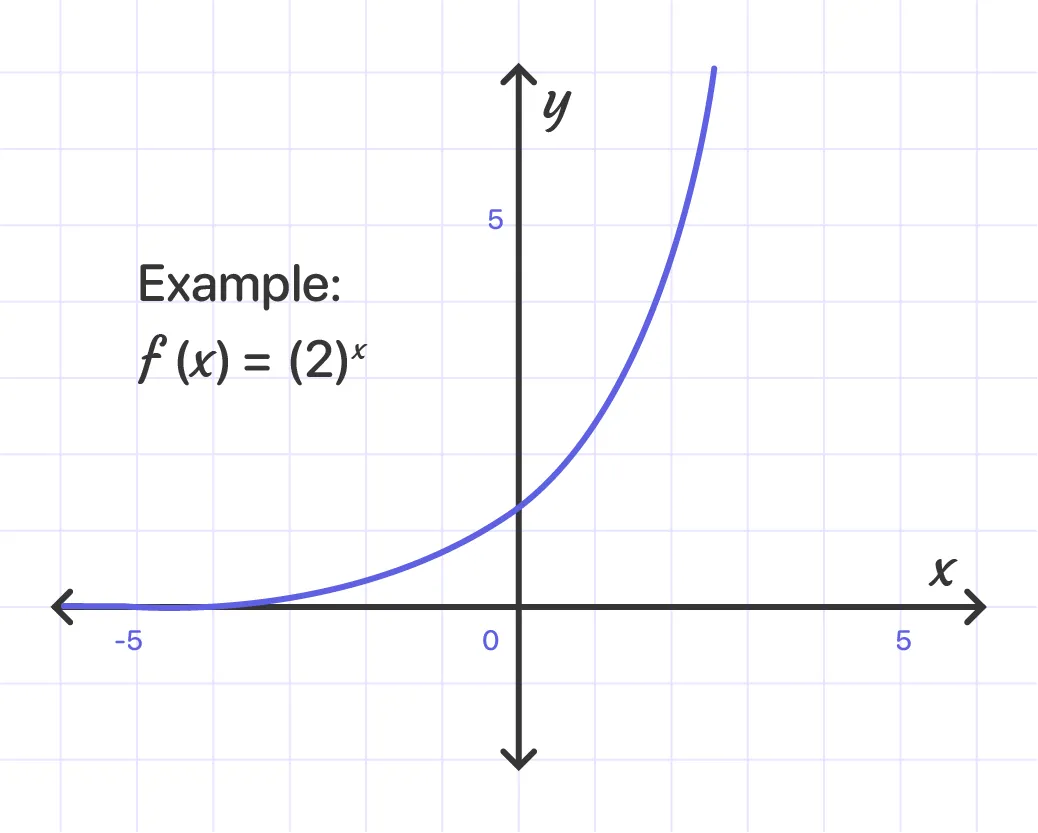
• When a is above 1, here’s the graph we have:

  

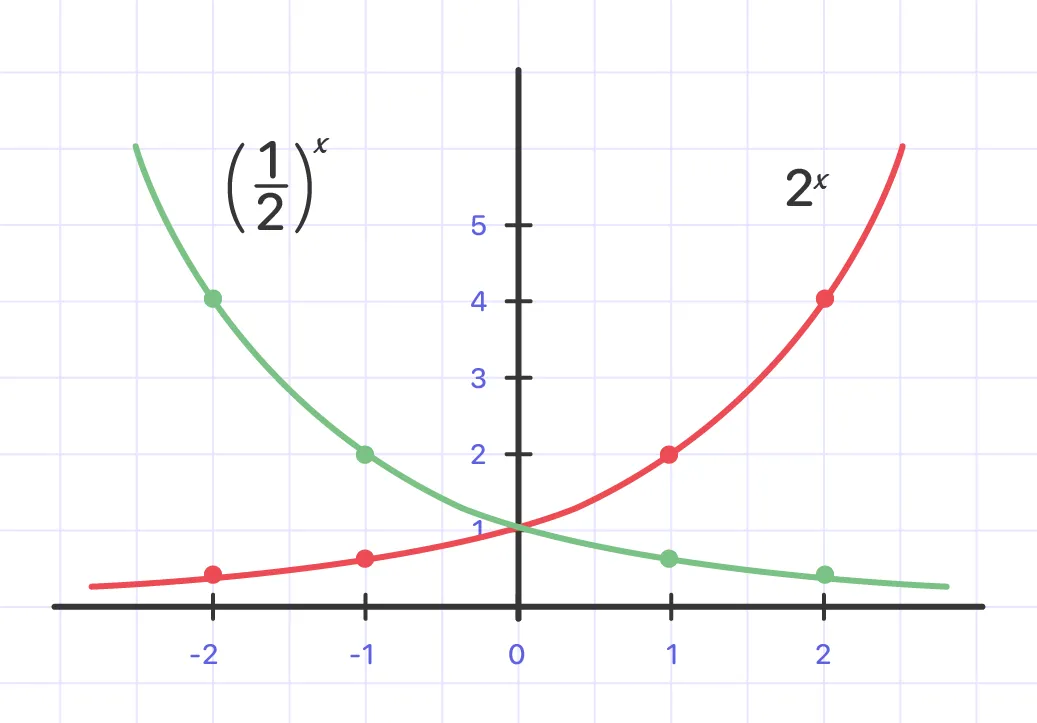
Example:

Sketch the graph of f(x) = 2^x and g(x) = $\(frac{1}{2})^x$ on the same axis system.

First, we have to pick some values of x and do some function evaluations.

Therefore, here is the sketch of the two graphs:

Example:

Sketch the graph of h(t) = $1 - 5e^{1 - \frac{t}{2}}$

Solution:

Step1:

Make a table of values for this function.

Step2:

Plot the graph.