Solving polygons

A polygon is a closed two-dimensional shape with three or more straight lines. At least three sides are required for a polygon.

Formulas for a regular polygon:

The sum of interior angles of a polygon is 180°(n-2);

The number of diagonals of an “n-sided” polygon = [n(n-3)]/2;

The measure of each interior angle of a regular n-sided polygon [(n-2)180°]/n;

The measure of exterior angles of a regular n-sided polygon = 360°/n;

Area of regular polygon = (number of sides x apothem x length of one side)/2, where apothem length is given as $\frac{I}{2tan(\frac{180}{n})}$ and where l is the side length of the regular polygon and n is the number of sides.

Example 1:

Trapezoid LMNO has parallel bases LM and NO. Line segment LM is 7 cm long, and line segment NO is 13 cm long. WE will label side NO as a and shorter side LM as b. The height (h) is 5 cm. Find the area of the trapezoid.

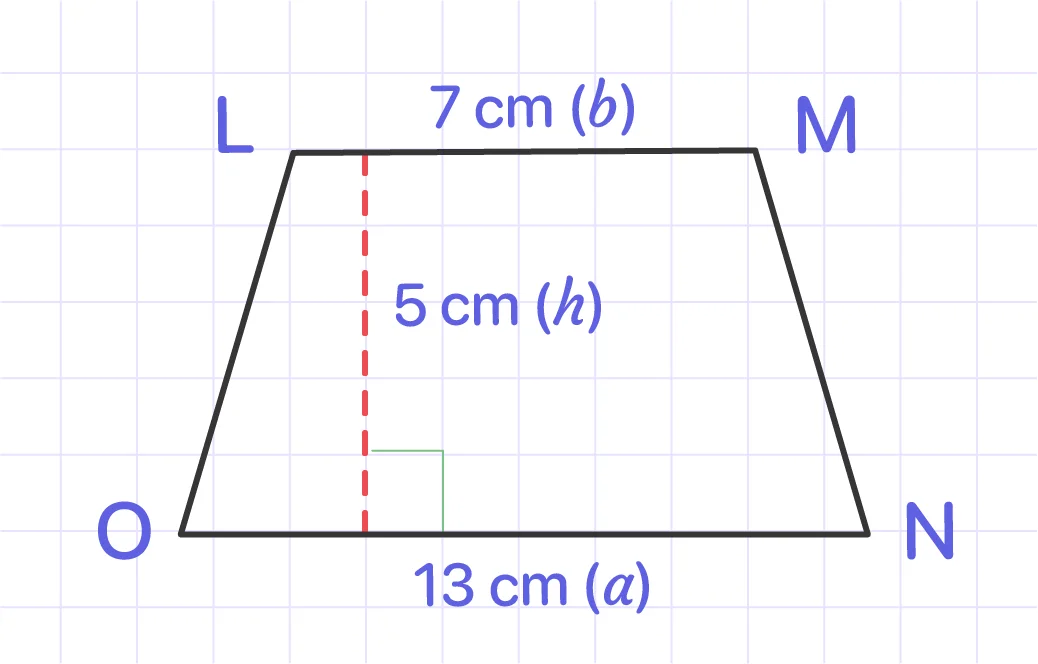
Solution:

The trapezoid area formula is $\frac{a + b}{2} \times h$. So,

Answer: The area of LMNO is 50 cm^2.

Example 2:

How many degrees are there at each angle of a regular hexagon?

a)60°

b)90°

c)108°

d)120°

e)144°

Solution:

A regular hexagon may be broken up into six equilateral triangles.

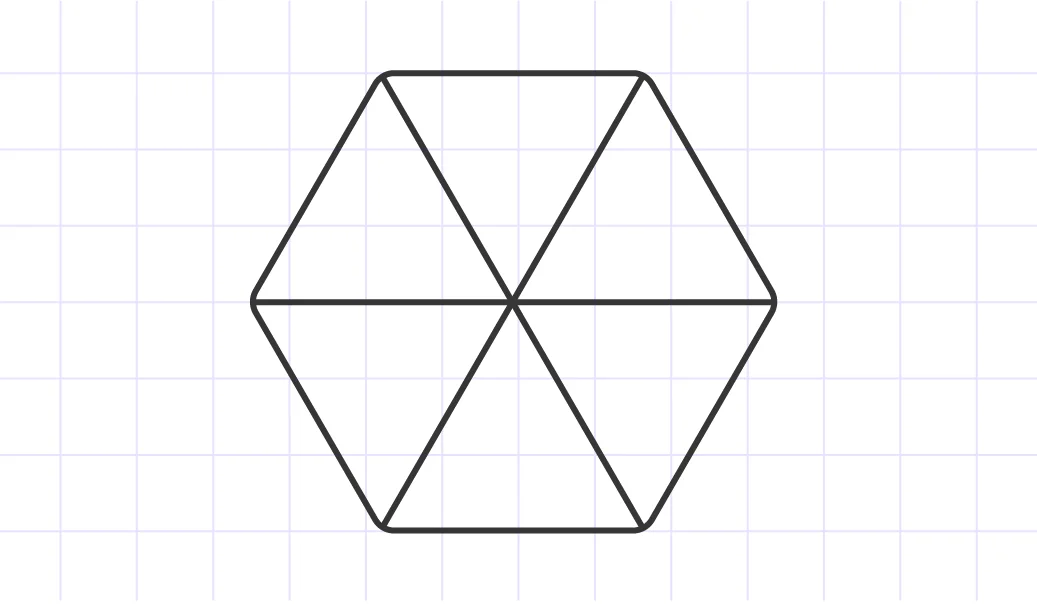
Since the angles of each triangle are 60°, and two of these angles make up each angle of the hexagon must be 120°.

Answer: d)120°

Example 3:

If each exterior angle of a regular polygon measures 40°, how many sides does it have?

Solution:

The sum of the exterior angles of any polygon is 360°. If each exterior angle measures 40°, then the polygon has 360/40 = 9 sides.

Answer: The polygon has 9 sides.

Example 4:

Find the sum of the interior angle of a hexagon.

Solution:

Using the polygon formula, we know that the sum of interior angles is given by:

Interior angle sum = 180°(n-2)

= 180°(6-2)

= 180° (4)

= 720°

Answer: The sum of the interior angles of a hexagon is 720°.

Example 5:

Use the formula (n - 2) x 180 to figure out the sum of the angle measures of the decagon.

Solution:

A decagon is a 10-sided polygon. So, n=10. The sum of the interior angles of a polygon is

(n-2) x 180

(10-2) x 180

8 x 180 = 1440

Answer: The measure of the decagon is 1440°.