MathMaster Blog
A system of equations is a group of one or more equations with several variables. To solve a system, you must identify all of the common solutions or points of intersection.
We require at least 2 equations to solve a system of equations in 2 variables. Similarly, we will need at least 3 equations to solve a system of equations in 3 variables.
3 ways to solve a system of equations:
Substitution Method:
express y in terms of x in one of the equations and then substitute it in the 2nd equation.
Elimination Method:
- Step 1: Eliminate one of the unknowns, by multiplying equations by suitable numbers, so that the coefficients of one of the variables become the same.
- Step 2: Subtract one equation from the other to find the value of one of the unknowns.
- Step 3: Substitute the value of the found unknown into one of the original equations to calculate the second unknown value.
- Step 4: To verify the correctness of the answer, take both values and substitute them in an equation that was not used to find the value of the second unknown.
Graphical Method:
plot the graphs of simultaneous equations to get the solution.
There can be different types of solutions to a given system of equations:
- Unique solution
- No solution
- Infinitely many solutions
Example 1:
x = 4 + 2y
2x - 4y = 5
2(4 + 2y) - 4y = 5
8 + 4y - 4y = 5
8 = 5
Answer: The given system of equations has no solution.
Example 2:
Solution of a system of equations with two variables by the graphical method.
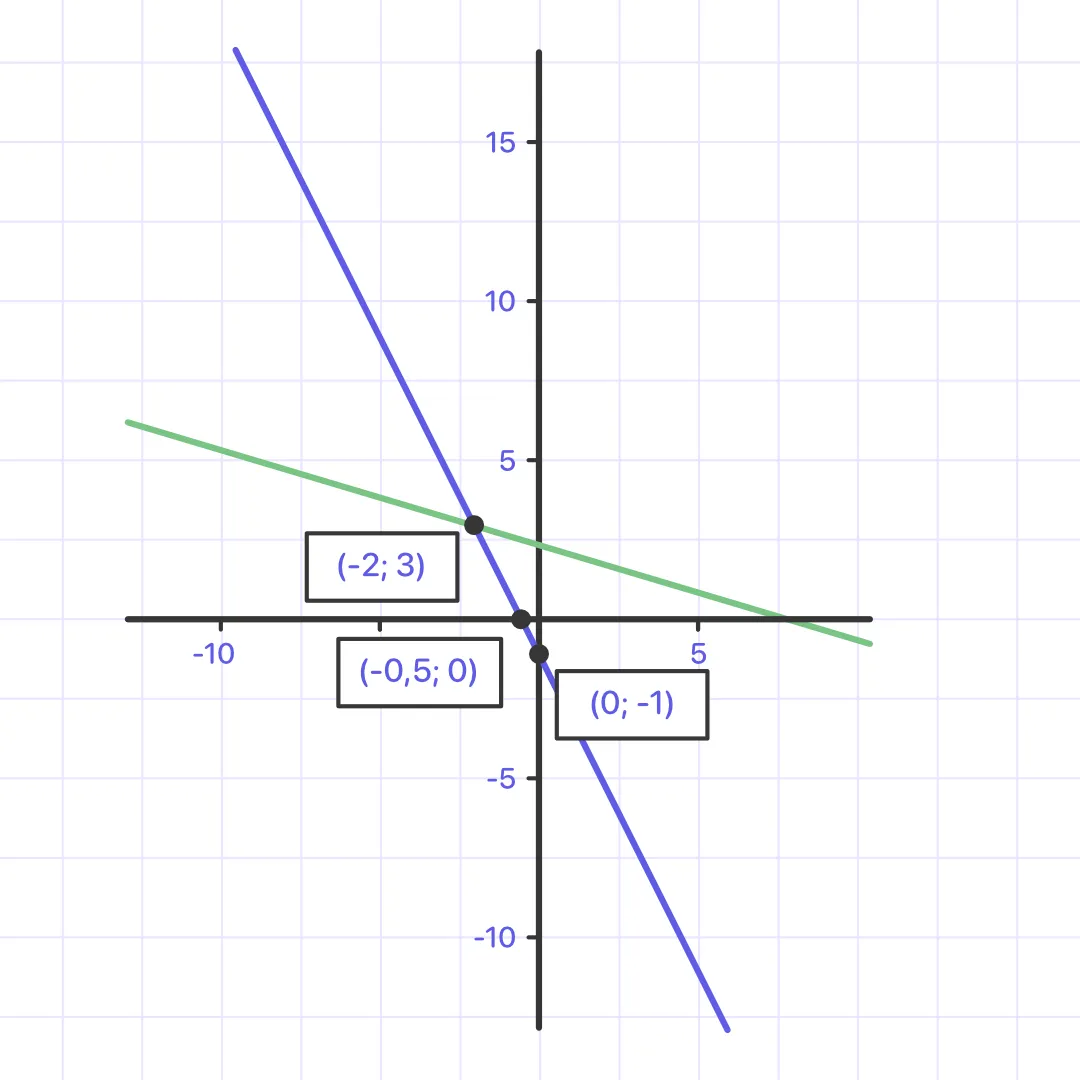
Solve and graph the system below:
x + 3y = 7
y = -2x - 1
Solution:
If there are two unknowns:
Both equations are taken and brought to the "y =" state so that we could draw a graph on the coordinate line.
The intersection points of these two graphs will be the answers.
Example 3:
If the system has exactly one solution, then k = ( ) ?
y = x^2- x + 9
y = kx
Solution:
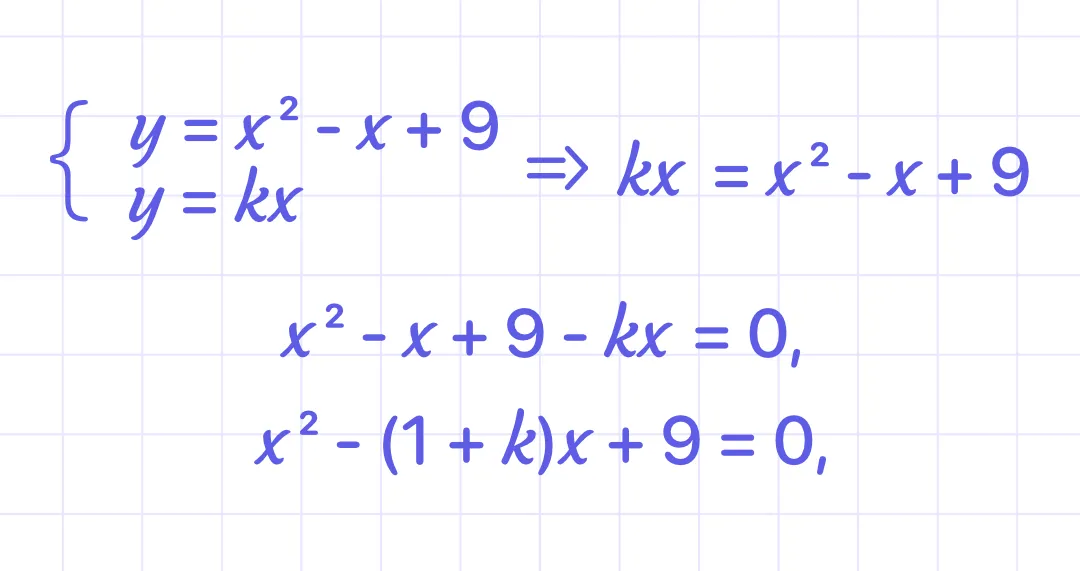
To have exactly one solution, the discriminant = 0

Answer: k = -7 or k = 5