MathMaster Blog

Probability is the study of events and how likely they are to happen.

It is usually represented as a fraction. The numerator shows the number of ways that the event can occur, whereas the denominator expresses the total number of possible events in a particular context.

Probability has 5 basic rules you should know:

#1: Probability is a numerical value that can be assigned to events and outcomes. It is always less than or equal to one and greater than or equal to zero.

#2: The probability of all possibilities must add up to 1. It can be expressed as P(S) = 1, where S represents the entire sample space.

#3: The Addition Rule: the probability that one of two occurrences happens is equal to the sum of their individual probabilities if they have no common outcome.

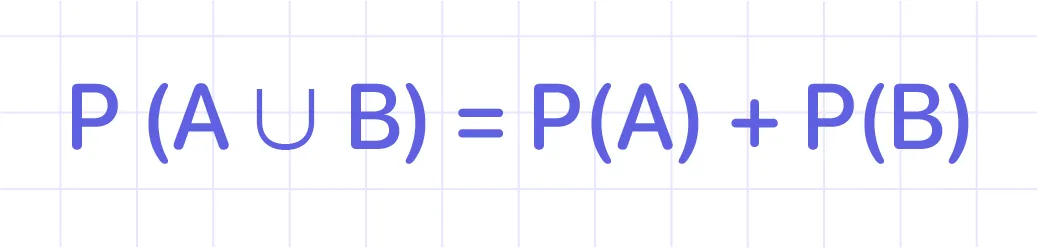
#4: The Complement Rule: the probability of an event not occurring is equal to 1 minus the probability of the event occurring.

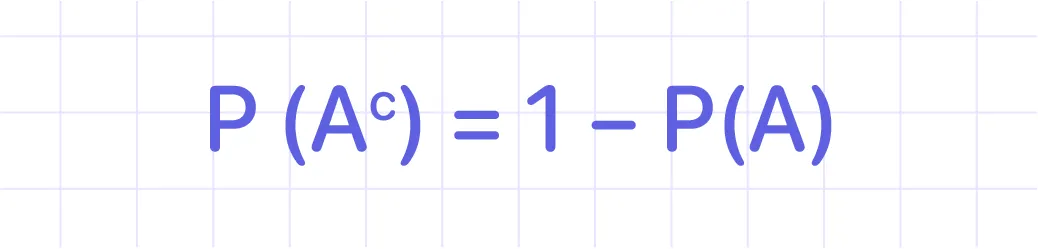
#5: When two events (A and B) are independent, we use this formula:

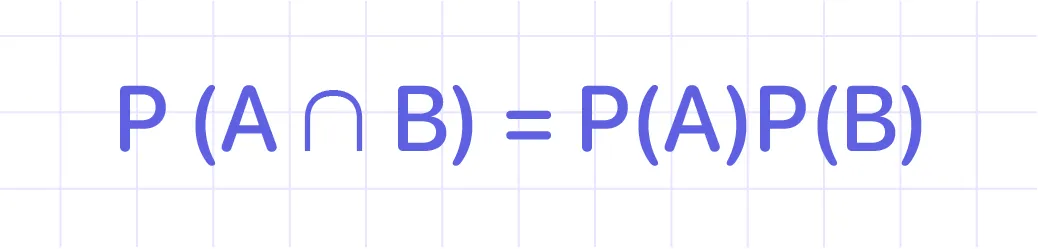
The probability formula can be expressed as:

• P(B) is the probability of an event 'B'.
• n(B) is the number of favorable outcomes of an event 'B'.
• n(S) is the total number of events occurring in a sample space.

Probability Tree Diagram

A tree diagram is a visual depiction that aids in determining the chance of an event happening or not happening.

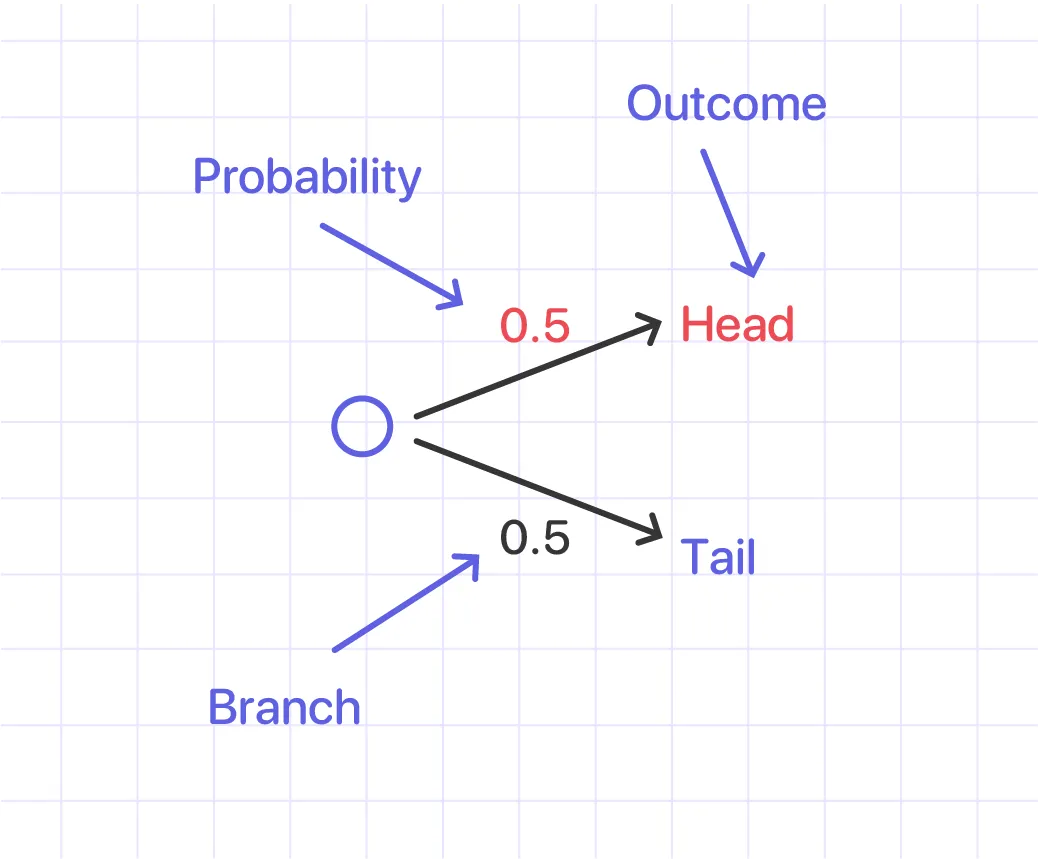
Example 1:

If one coin is tossed twice, what is the probability of getting a head?

Solution:

Let S represent the sample space.

Draw a tree diagram that depicts a coin tossing twice.

S = {HH, HT, TH, TT}

The probability of getting a head is P(HT) = 1/4 = 0.25.

Answer: 0.25

Example 2:

When a coin was tossed, it landed 12 times on heads and 8 times on tails. What was the percentage of times it came up tails?

Solution:

Compare the number of tails and the number of tosses.

8/20 = 0.40 or 40%

Answer: 40%