MathMaster Blog

How to compare rational numbers

Method 1: Use a number line. The farther right you go, the greater the value.

Method 2: Write both numbers in the same form – as fractions or as decimals.

Method 3: If the numbers are fractions, write them to have a common denominator.

Example:

Compare 0.2 and – 0.4.

Solution:

Draw a number line.

Since 0.2 is positive and – 0.4 is negative, 0.2 is greater than – 0.4.

Answer: 0.2 > –0.4.

How to order rational numbers

Ordering rational numbers means to get rational numbers in order from least to greatest, or from greatest to least.

You can order rational numbers using the comparing rational numbers methods:

Method 1: Use a number line. The farther right you go, the greater the value.

Method 2: Write both numbers in the same form – as fractions or as decimals.

Method 3: If the numbers are fractions, write them to have a common denominator.

Example:

Put $\frac{3}{5}, -2\frac{4}{5}, \frac{1}{2}, 3\frac{2}{7}$ in order from least to greatest.

Solution:

Step1:

Rewrite each fraction as a decimal

$\frac{3}{5} = 0.6, -2\frac{4}{5} = -2.8, \frac{1}{2} = 0.5, 3\frac{2}{7} = 3.285714286$

Step2:

– 2.8 is the only negative number, so it will go first.

Next, consider the unit's place. Two numbers have a 0, and one has a 3. Since 0 is smaller than 3, those two numbers will go next.

Now look at the tenths place for those two numbers. There is a 6 in one number and a 5 in the other number. Since 5 < 6, 0.5 will come next, and then 0.6.

0.5, 0.6

The last is 3.285724386.

So, here’s the order from the least to the greatest

–2.8, 0.5, 0.6, 3.285714286 or $-2\frac{4}{5}, \frac{1}{2}, \frac{3}{5}, 3\frac{2}{7}$

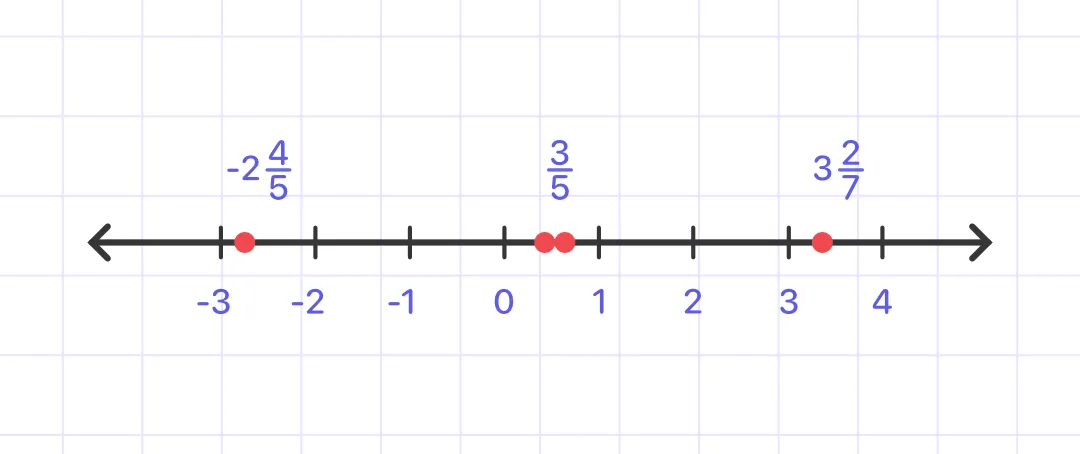
Answer: $-2\frac{4}{5}, \frac{1}{2}, \frac{3}{5}, 3\frac{2}{7}$