Compound amount & Compound interest

Compound interest is interest earned on both the principal and interest over a certain time period. After determining the entire amount over a period of time, based on the rate of interest and the beginning principal, compound interest can be calculated.

Compound amount formula:

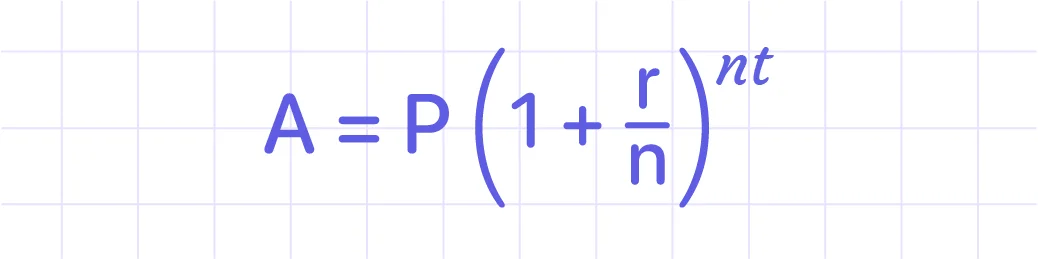
A = Future value

P = Principal (the initial amount)

r = annual interest rate expressed as a decimal

n = amount of times the interest is compounded per time period

t = time period

By subtracting the principal from this amount, we may calculate compound interest.

Compound interest formula:

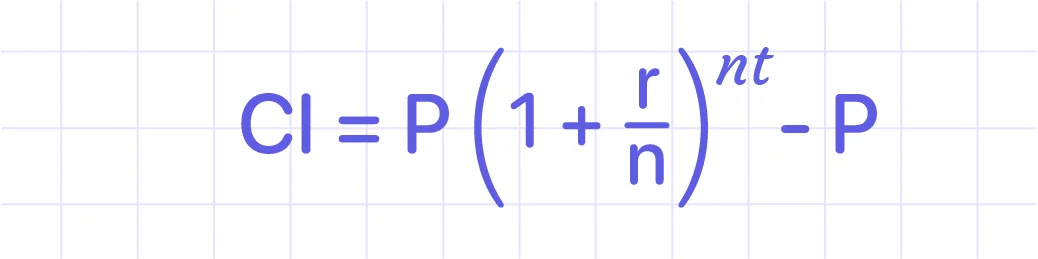
Example 1:

Adina invests £3200 into a savings account which has an interest rate of 3.2% per year.

Calculate the amount she would have in her account after 3 years if she leaves the money as it is.

Solution:

By compound amount formula:

A = P(1 + (r/100))^3

= 3200 x (1+(3.2/100))^3

= 3200 x (1.0323^3)

= 3517.1353 pounds

Answer: A = £3517.1353

Example 2:

Noah gives Emma a loan of $4000 at a rate of 10% per year compounded half-yearly for a duration of two years. Can you assist him in determining how much money he receives from Emma after a two-year period? Apply the compound interest formula to this problem.

Solution:

Input the given data to the compound interest formula:

A = P(1+{r / 2}/100)^(2n) =

= 4000(1+{10 / 2}/100)^(2(2))= $4862.03

Answer: A = $4862.03