MathMaster Blog

A repeating decimal is a number that repeats the same ending digit or pattern of ending digits forever. The repeating digits are represented by lines over the first and last repeating digits.

0.123 = 0.1232323...

0.3 = 0.333333333...

Example 1:

Rewrite 0.7 as a simplified fraction.

Solution:

Step1:

Let x equal the decimal

x = 0.77777…

Step2:

Set up a second equation such that the digits after the decimal point are identical:

10x = 7.7777…

x = 0.7777…

Step3:

Subtract two equations and solve for x

9x = 7

x = 7/9

Answer: 0.7 = 7/9

Example 2:

Convert 4/9 to a decimal

Solution:

Apply the long devision method:

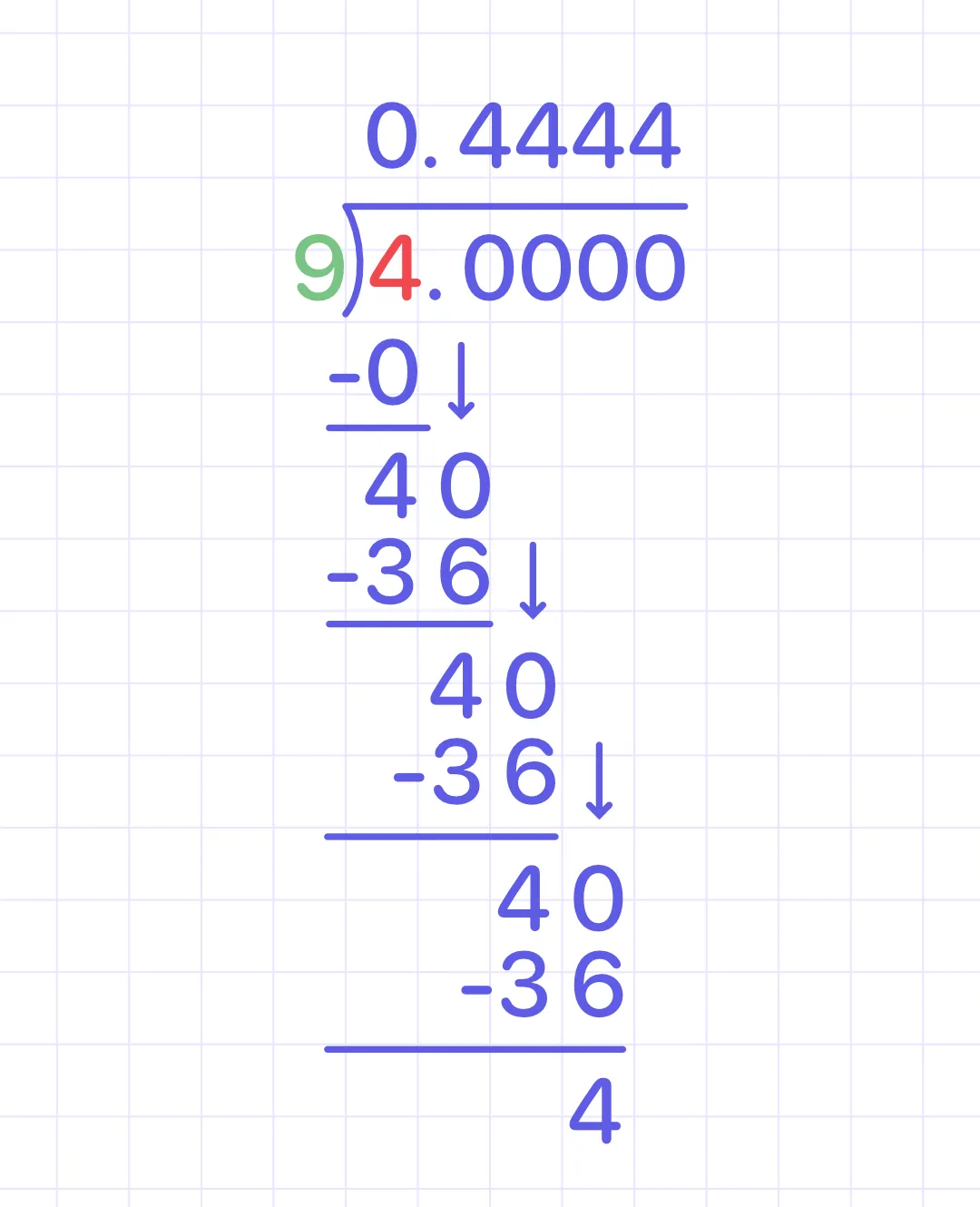
No matter how long we divide, the 4 will continue to repeat in the quotient.

Answer: 4/9 = 0.4/p>