MathMaster Blog

Apply the Distributive Property rule to expand the expression. Then, combine like terms (monomials that have the same variables raised to the same exponents).

Example:

Expand 7(2n + 4).

Solution:

Multiply the term outside the parentheses (7) by each term inside the parentheses.

Then, add

7(2n) + 7(4) = 14n + 28

Answer: 7(2n + 4) = 14n + 28

Expanding binomials

A binomial is an expression with two terms.

To multiply two binomials, multiply each term in the first binomial by each term in the second binomial.

Use the FOIL method:

Find the products of the First, Outside, Inside, and Last terms. Then combine those products.

Example:

Expand (5a – 3b)(2a + 4b).

Solution:

Step1:

Rewrite the expression substituting subtraction with addition

(5a + -3b)(2a + 4b)

Step2:

Apply the FOIL method

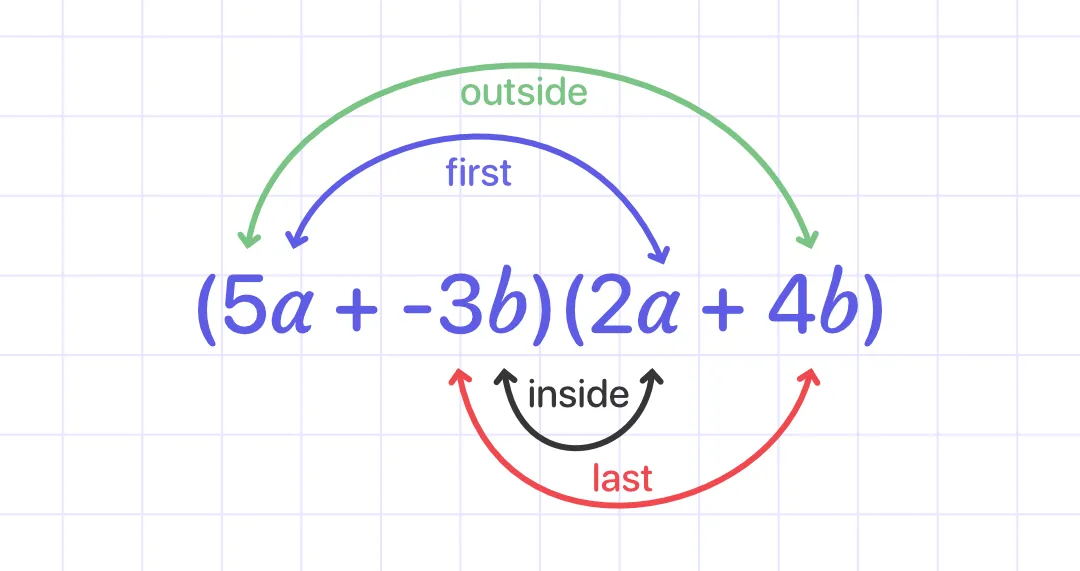
Step3:

Calculate the products

5a(2a) = 10a^2

5a(4b) = 20ab

–3b(2a) = -6ab

–3b(4b) = -12b^2

Step4:

Combine the products and simplify by combining like terms

10a^2 + 20ab + -6ab + -12b^2

10a^2 + 14ab + -12b^2

Step5:

Rewrite using the negative sign

10a^2 + 14ab - 12b^2

Answer: (5a – 3b)(2a + 4b) = 10a^2 + 14ab - 12b^2