MathMaster Blog

An exponent is a number that shows the repeated multiplication of a base.

Properties of exponents can help simplify expressions with exponents.

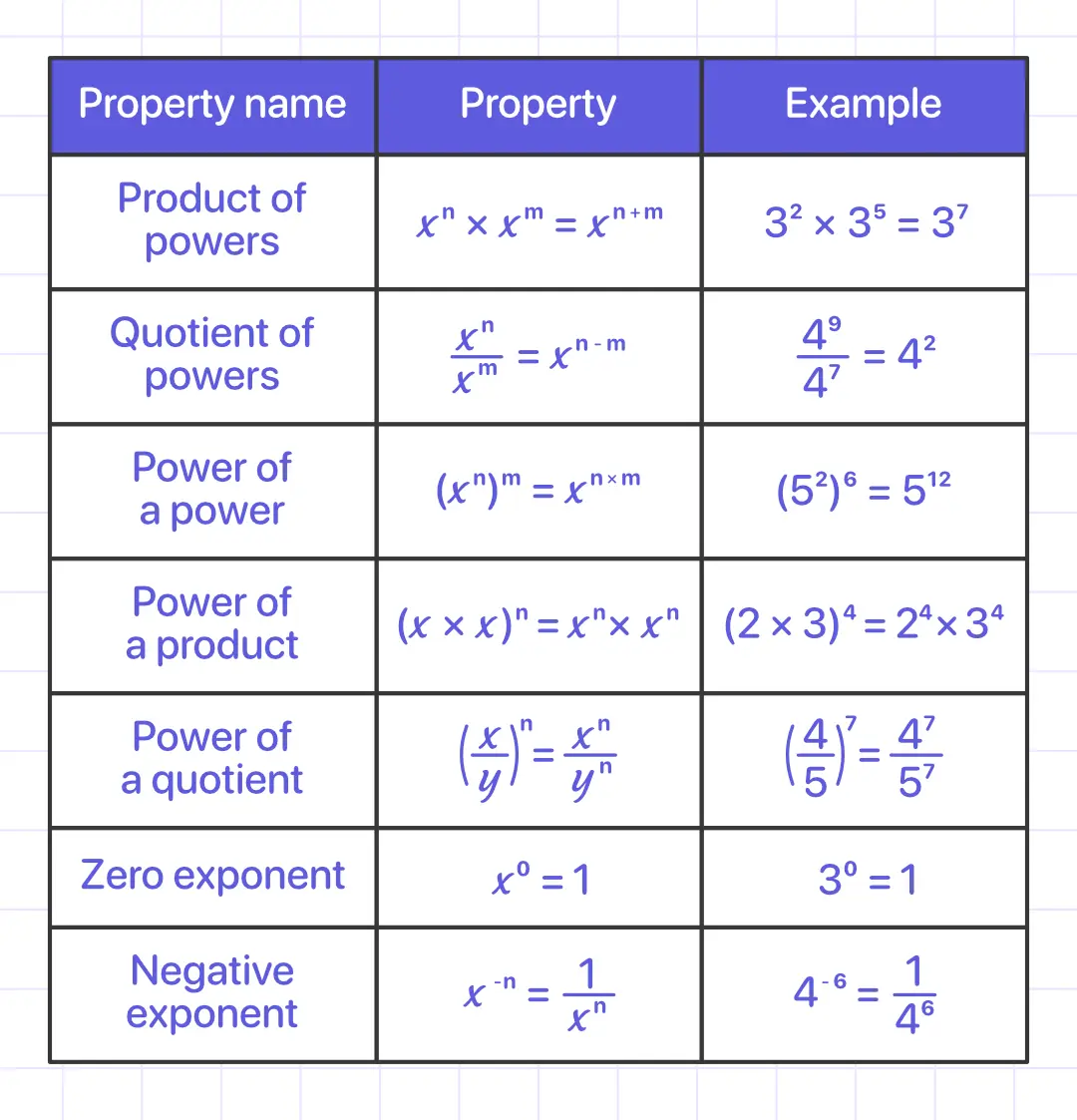
Product of Powers

Example:

Find $974^4 \cdot 974^6$

Solution:

To multiply powers with the same base, add their exponents. Then, simplify the expression.

$974^{4+6}$

Answer: $974^{10}$

Quotient of Powers

Example:

Find $\frac{875^8}{875^7}$

Solution:

To divide powers with the same base, subtract their exponents. Any number to the first power is equal to itself.

$\frac{875^8}{875^7}$ = $875^{8-7}$ = $875^1$

Answer: $875^1$

Power of a Power

Example:

Simplify $3^{6^5}$

Solution:

To raise a power to a power, multiply the exponents.

$3^{6^5}$ = $3^{6 \cdot 5}$ = $3^{30}$

Answer: $3^{30}$

Power of a Product

Example:

Simplify $(p \times y)^{35}$

Solution:

To find the power of a product, multiply the powers of the individual factors.

$(p \times y)^{35}$ = $p^{35} \times y^{35}$

Answer: $p^{35} \times y^{35}$

Power of a Quotient

Example:

Simplify $(\frac{x + 1}{4x})^2$

Solution:

To find the power of a quotient, divide the powers of the numerator and denominator.

$(\frac{x + 1}{4x})^2$ = $\frac{(x + 1)^2}{(4x)^2}$

Now, simplify

$\frac{x^2 + 2x + 1}{16x^2}$

Answer: $\frac{x^2 + 2x + 1}{16x^2}$

Negative Exponent

Example:

Simplify $(\frac{t^{-3}}{4^2})^{-4}$

Solution:

When you see a base with a negative exponent, you can turn it into a fraction with a numerator of 1 and a positive exponent in the denominator.

$(\frac{t^{-3}}{4^2})^{-4}$ = $\frac{1}{t^3 \cdot 4^2}^{-4}$ = $(4^2 \cdot t^3)^4$

Now, apply the Power of a Power property

$(4^2 \cdot t^3)^4$ = $4^8 \cdot t^{12}$

Answer: $4^8 \cdot t^{12}$