MathMaster Blog

An exponential equation is one with exponents in which the exponent (or a part of the exponent) is a variable. Exponential equations are classified into three categories:

• with the same bases on both sides: 4^x = 4^2
• with different bases can be made the same: 4^x= 16 which can be written as 4^x = 4^2
• with different bases that cannot be made the same: 4^x = 15.

When the bases on both sides of the equation are not the same, we use logarithms to solve the exponential equations.

For example, neither the bases on both sides of 5^x = 3 are the same, nor can the bases be made the same. In such instances, one of the following options is available.

In these instances, we have such options:

1. Using the given formula we can transform the exponential equation to logarithmic form and then solve it for the variable.

   

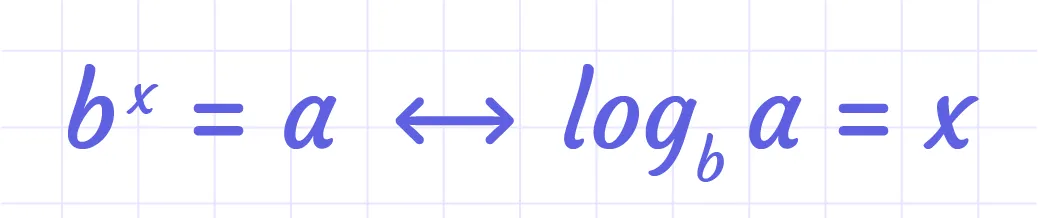
2. Use logarithm (log) on both sides of the equation and solve for the variable. In this case, we have to apply:

   

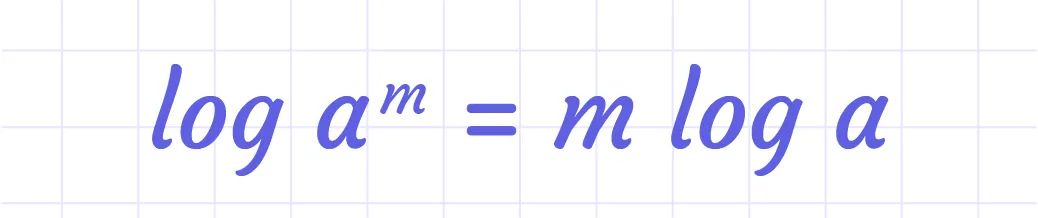
Example:

If we turn 5^x = 3 into the logarithmic form, we get log 5^3 = x. Applying the change of base property formula,

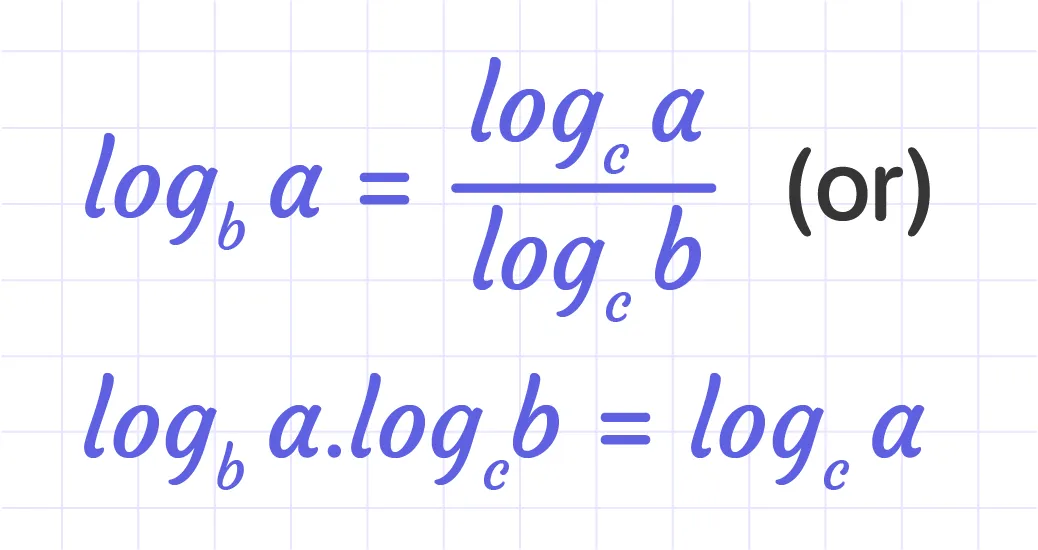
We have x = (log 3)/(log 5).