MathMaster Blog

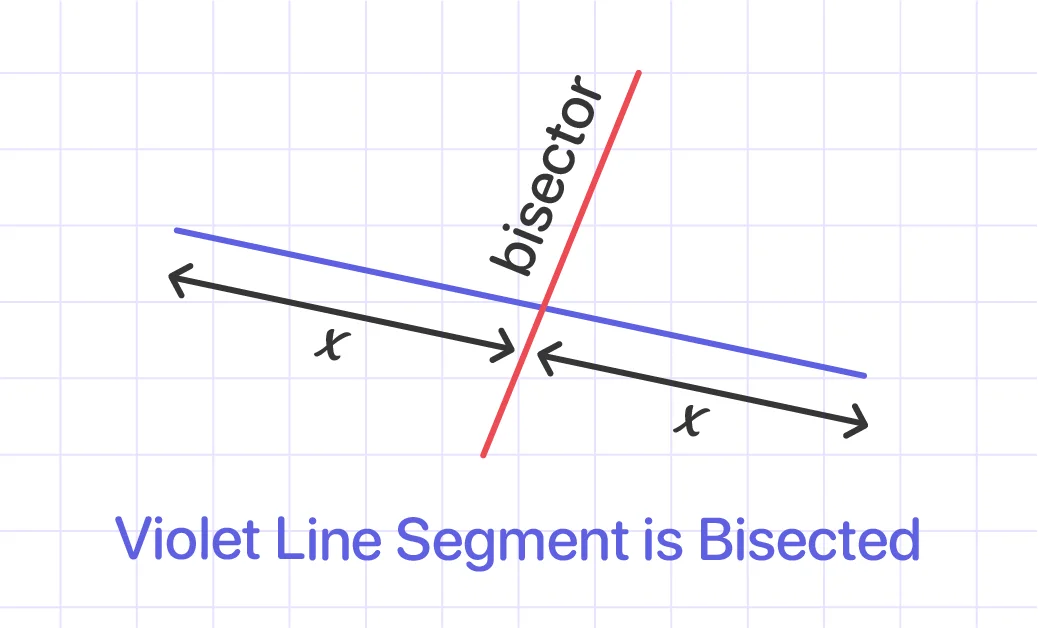
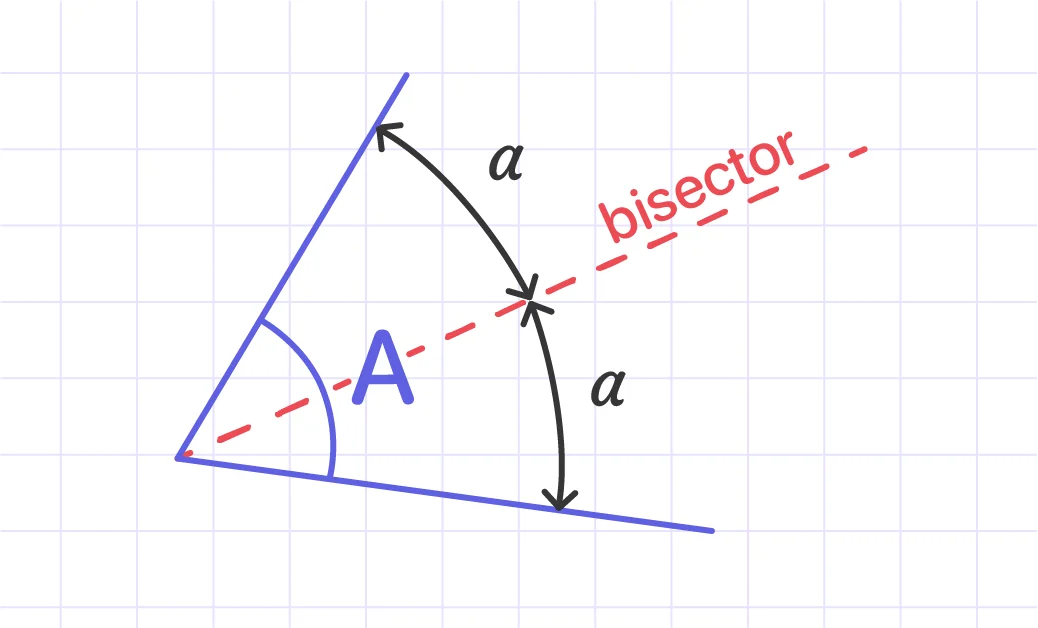
The term ‘bisect’ refers to dividing angles/shapes/lines into two equal halves. The dividing line is called the bisector.

Example 1:

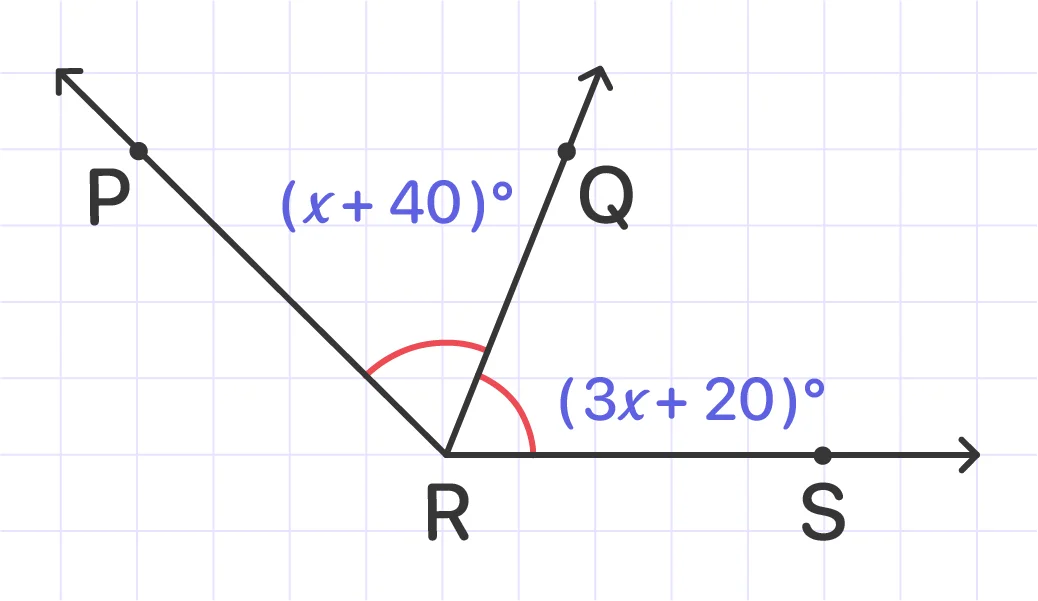
Find the value of x, knowing that RQ bisects the angle ∠PRS.

Solution:

Since RQ bisects the angle ∠PRS, ∠PRQ = ∠QRS, therefore, we can solve for x:

x + 40 = 3x - 20

40 + 20 = 3x - x

2x = 60

x = 30

Answer: The value of x is 30.

Example 2:

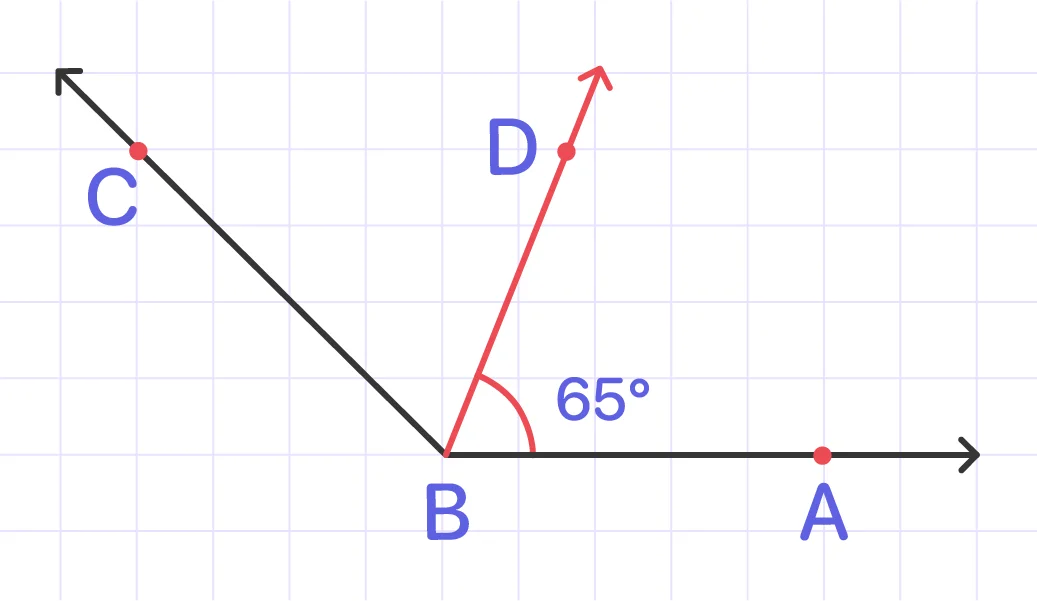
BD is an angle bisector. Find the measure of ∠ABC.

Solution:

Since BD is an angle bisector, m ∠CBD = m∠ABD

Therefore, m∠CBD = 65°

According to the Angle Addition Postulate, when two or more angles are placed side by side with a shared vertex and a common arm between each pair, the total sum of those angles equals the entire sum of the resulting angle.

Therefore, m∠ABC = m∠ABD + m∠CBD.

Now, we have to substitute:

m∠ABC = 65° + 65° = 130°

Answer: ∠ABC = 130°

Example 3:

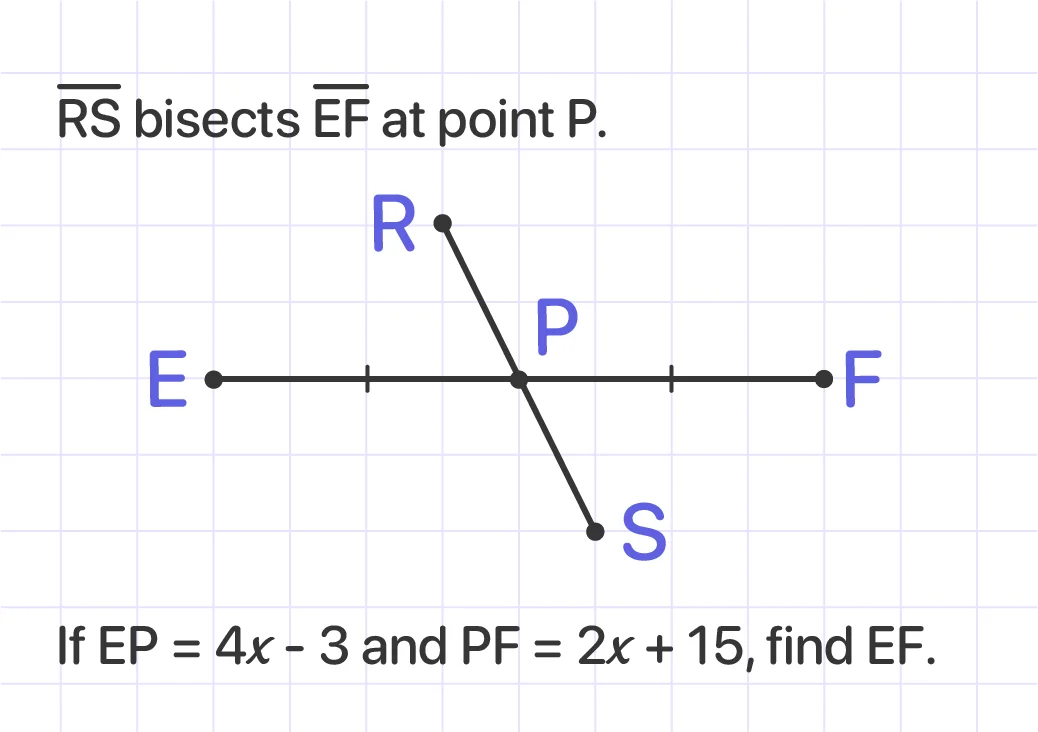
RS bisects EF at point P.

If EP = 4x - 3 and PF = 2x + 15, find EF.

Solution:

Since EP = PF,

4x - 3 = 2x + 15

4x = 2x + 18

2x = 18 and x = 9

EP = 4x - 3 = 4(9) - 3 = 36 - 3 = 33

EF = 2(EP) = 2(33) = 66

Answer: EF = 66