MathMaster Blog
In a two-dimensional plane, the area of a triangle is defined as the total space filled by its three sides. We should express the area of a triangle in square units (m^2, cm^2, in^2, etc.)
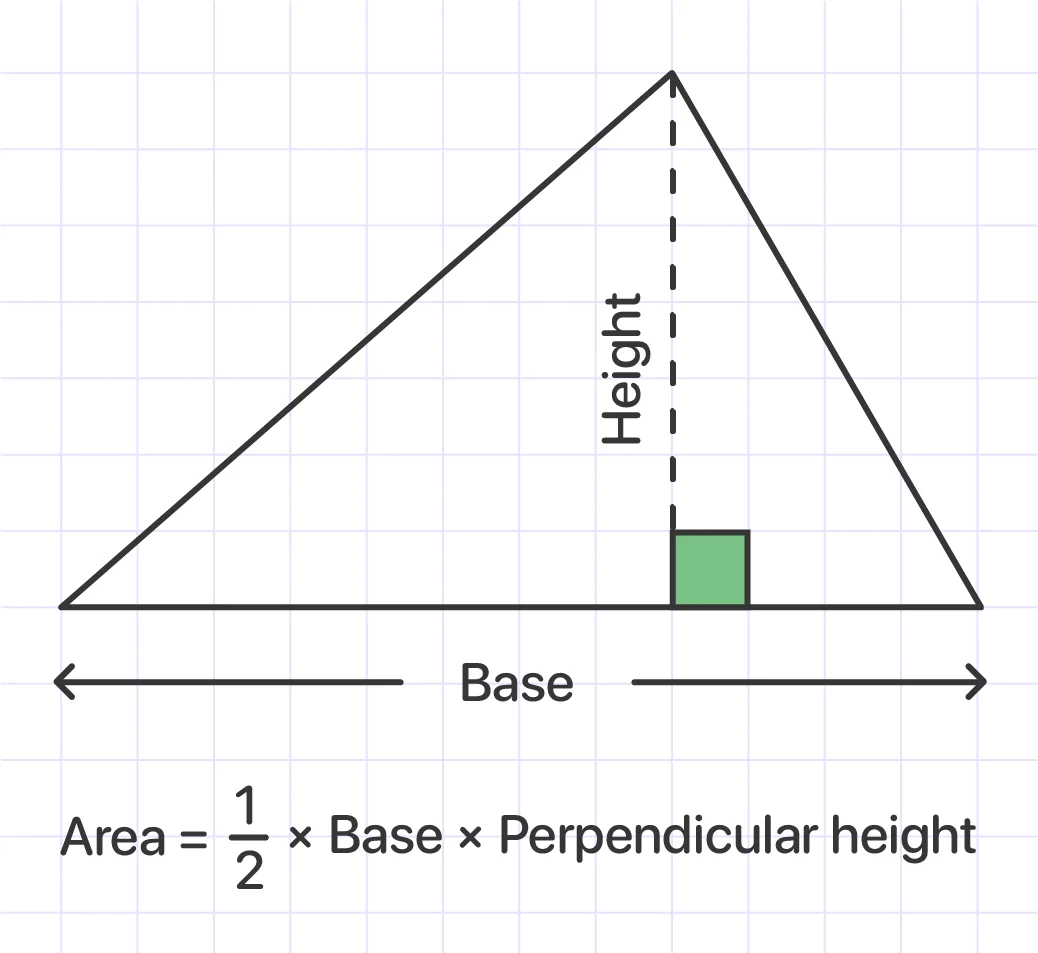
The basic formula used to find the area of a triangle:
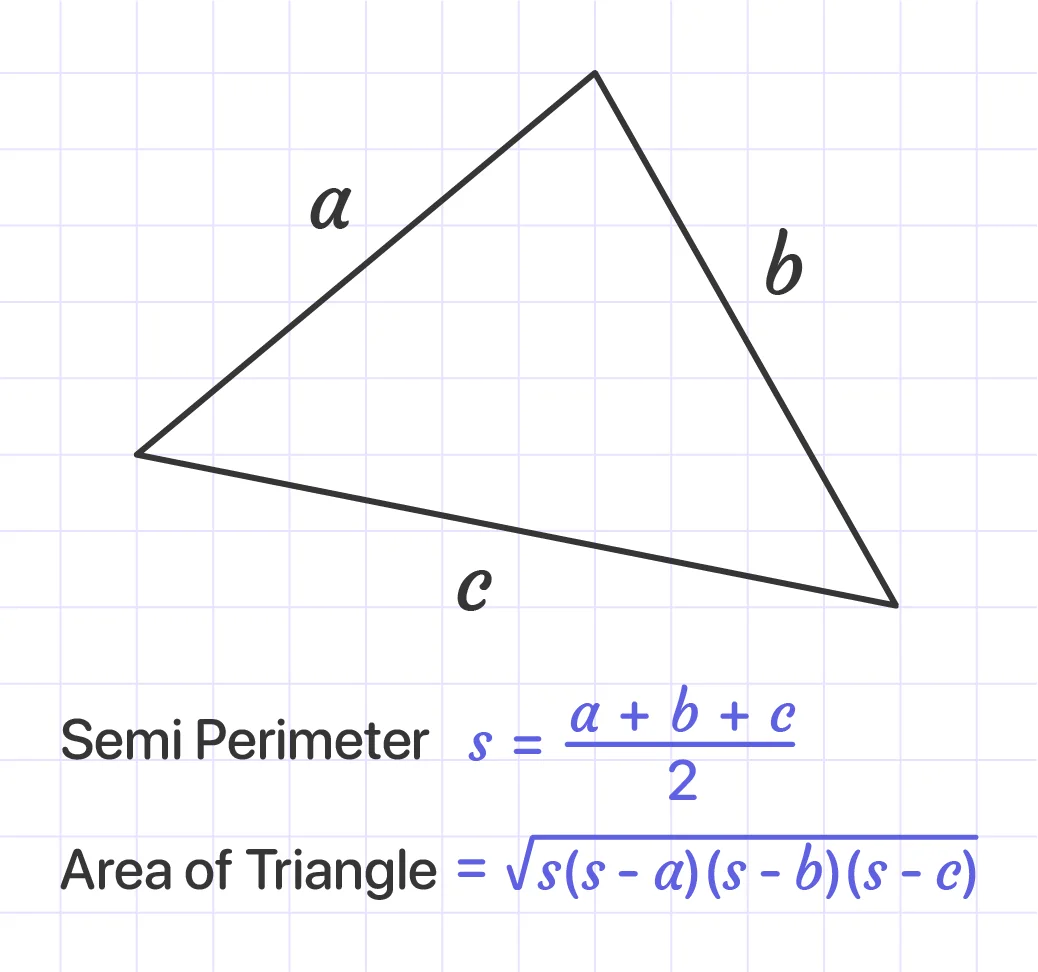
Heron's Formula to calculate the area of a triangle:
When the lengths of the triangle's three sides are known, we should apply Heron's formula to calculate its area. To use this formula, we determine the triangle's perimeter first.
When two sides and the included angle are given:

where θ is the angle between the given two sides.
When base and height are given:

An equilateral triangle with one side given:
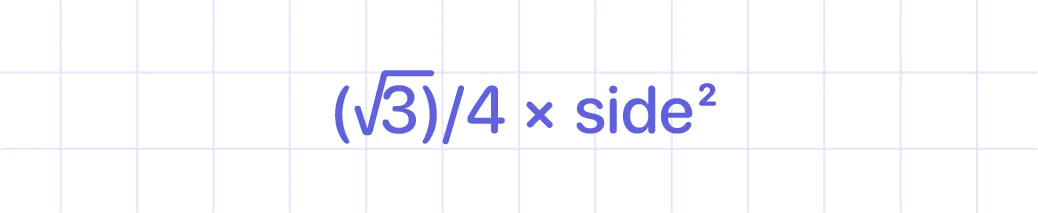
An isosceles triangle with an equal side and base known:

where b is the base and a is the length of an equal side.
Example 1:
Find the area of a triangle with a base of 8 cm and a height of 7 cm.
Solution:
Area of triangle = (1/2) × b × h
A = 1/2 × 8 × 7
A = 1/2 × 56
Answer: 28 cm2
Example 2:
Find the area of the triangle.
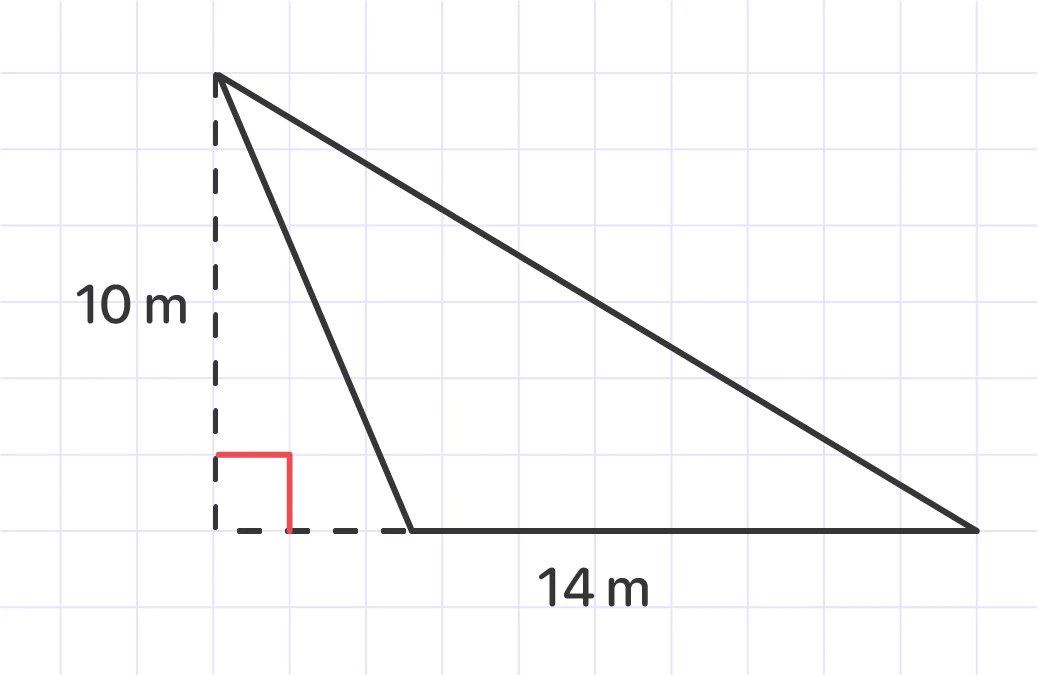
Solution:
Use the formula for calculating a triangle's area (A):
½ x base x height
Substitute 14 for b and 10 for h in the formula.
(1/2) × 14 × 10
Answer: A = 70
Example 3:
Calculate the area of an equilateral triangle whose each side is 12 in.
Solution:
Use the equilateral triangle area formula:
$\sqrt{3/4} \times (Side)^2$
= $\sqrt{3/4} \times (12)^2$
= $36\sqrt{3} in^2$
Answer: 36√3 in^2
Example 4:
What is the area of an equilateral triangle if its perimeter is 30 inches?
- 50
- 25
- 50$\sqrt{3}$
- 25$\sqrt{3}$
- 10$\sqrt{3}$
Solution:
In an equilateral triangle with a perimeter of 30 inches, each side has a length of 10 inches.
So, we should calculate the area using this formula:
$\sqrt{3}/4 \times (Side)^2$
= $\sqrt{3}/4 \times (10)^2 = 25\sqrt{3}inch^2$
Answer: 25√3 inch^2, 4)
Example 5:
Find the base length of an isosceles triangle with an area of 243 cm^2 .
Solution:
Height of the triangle (h) = 9 cm
The base of the triangle = b =?
We should use the formula (1/2) × b × h to calculate the area of an isosceles triangle.
243 = (½) x b x 9
243 = (b x 9)/2
b = (243 x 2)/9
b = 54 cm
Answer: A = 54 cm