MathMaster Blog

To solve a triangle, you must be aware of all three sides as well as all three angles. In right triangles, trigonometric functions can be used to find missing side lengths.

The three trigonometric functions most often used to solve for a missing side of a right triangle are:

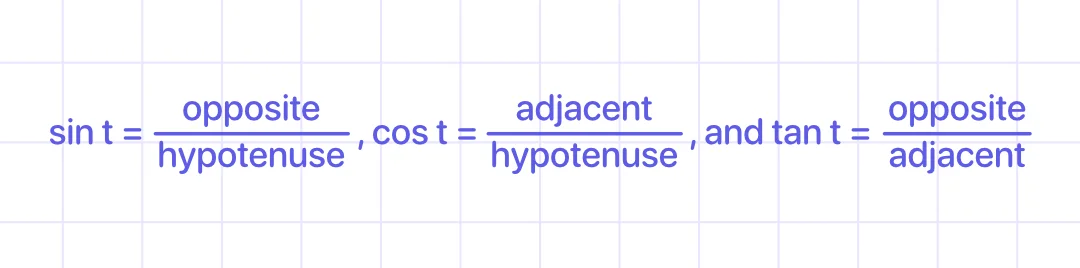
When solving for a missing side, the first step is to identify what sides and what angles are given and then select the appropriate function to solve the problem.

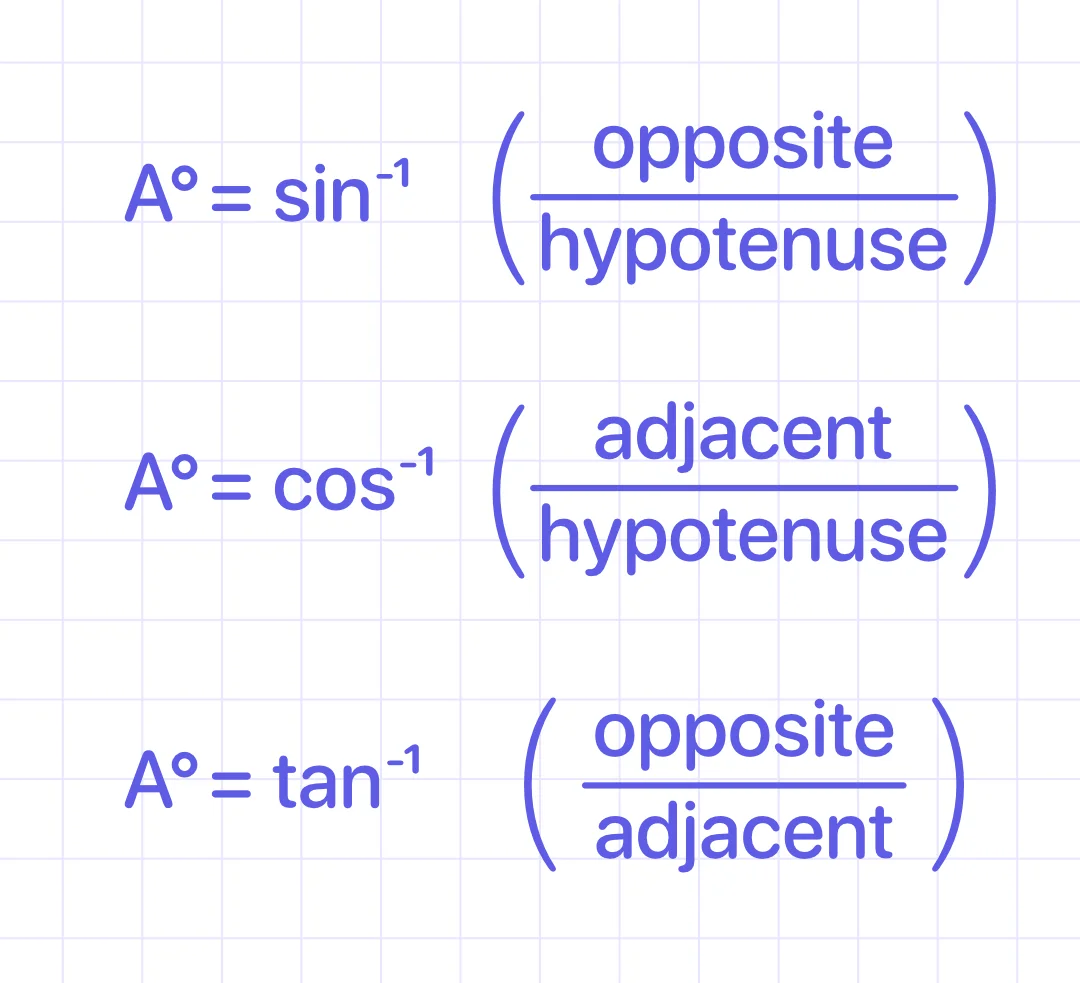
The acute angle measurement of a right triangle can be calculated using inverse trigonometric functions.

To find a missing angle value, use the trigonometric functions sine, cosine, or tangent, and the inverse key on a calculator to apply the inverse function:

Example 1:

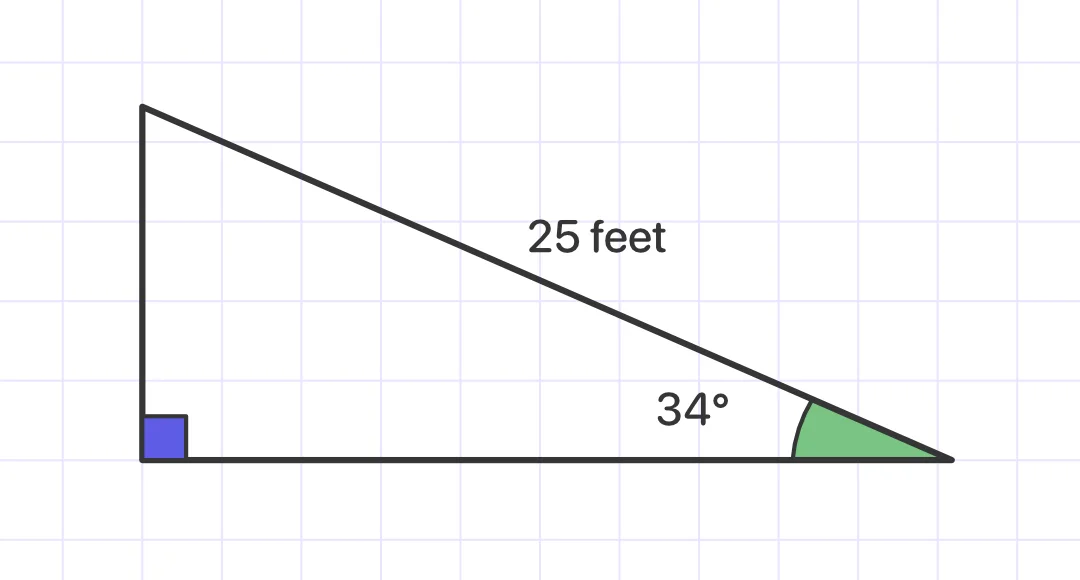
Given a right triangle with an acute angle of 34∘ and a hypotenuse length of 25 feet, find the length of the side opposite the acute angle (round to the nearest tenth):

Solution:

The ratio of the sides would be the opposite side and the hypotenuse. The ratio that relates to those two sides is the sine function.

sin t = opposite/hypotenuse

sin 34 = x/25

25 x sin (34°) = x

x = 25 x sin (34°)

x = 25 x (0.559…)

x = 14.0

Answer: The side opposite the acute angle is 14.0 feet.

Example 2:

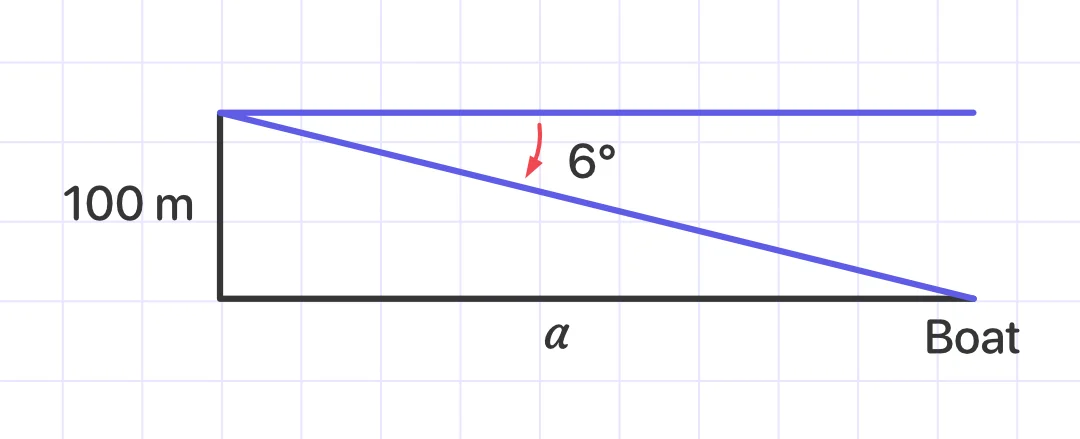
Find the distance between a boat and a lighthouse if the lighthouse is 100 meters tall and the angle of depression is 6°.

Solution:

The lighthouse keeper must look down 6 degrees to view the boat.

The triangle created by the lighthouse and the distance d between the lighthouse and the boat is now right-angled. Because the angle of depression is 6°, the alternate angle is also 6°.

If d is the distance of a boat from the lighthouse, then

d/100 = cot 6° = 9.514

Answer: The distance is d = 951.4 meters.